Next: About this document ... Up: Appendix Previous: Bode Plots of Components
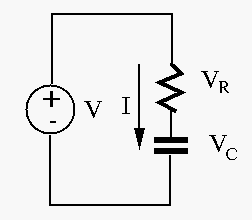
 across C is treated as output. According to voltage
divider rule, we have:
across C is treated as output. According to voltage
divider rule, we have:
 |
(530) |
 .
.
 across R is treated as output:
across R is treated as output:
 |
(531) |
 can be written as:
can be written as:
 |
(532) |
 . Now the log-magnitude is:
. Now the log-magnitude is:
 |
(533) |
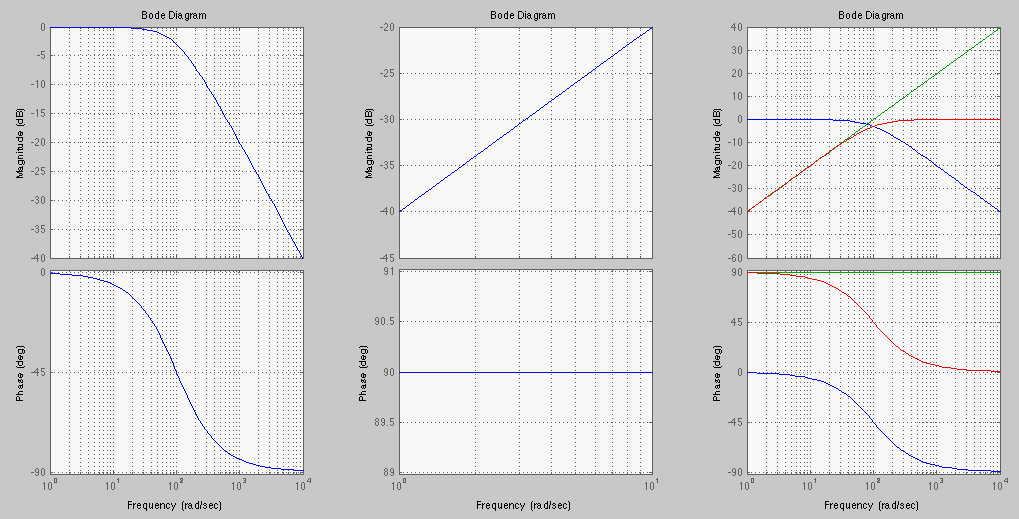
 and the second plot is a straight line
with slope of 20 dB/dec. at
and the second plot is a straight line
with slope of 20 dB/dec. at
 , the first term is -3 dB and the
second is 0 dB. The phase plot is:
, the first term is -3 dB and the
second is 0 dB. The phase plot is:
 |
(534) |
 ,
,
 rad/sec.
rad/sec.
Define






Second order circuits
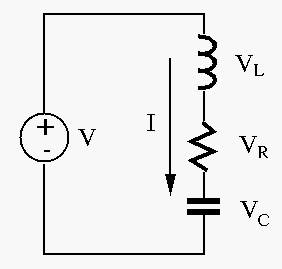
 across C is treated as output:
across C is treated as output:
 |
 |
 |
|
 |
 |
(535) |
 |
(536) |
 |
(537) |
 . When
. When
 or
or
 , we have
, we have
 |
(538) |
 across R is treated as output:
across R is treated as output:
 |
 |
 |
|
 |
 |
(539) |
 |
(540) |
 , its value is
, its value is
 . The phase is
. The phase is
 for all
for all  .
.
The denominator can be written as




 across L is treated as output:
across L is treated as output:
 |
 |
 |
|
 |
 |
(541) |
 |
(542) |
 , it's value is
, it's value is
 . The phase is
. The phase is
 for all
for all  .
.
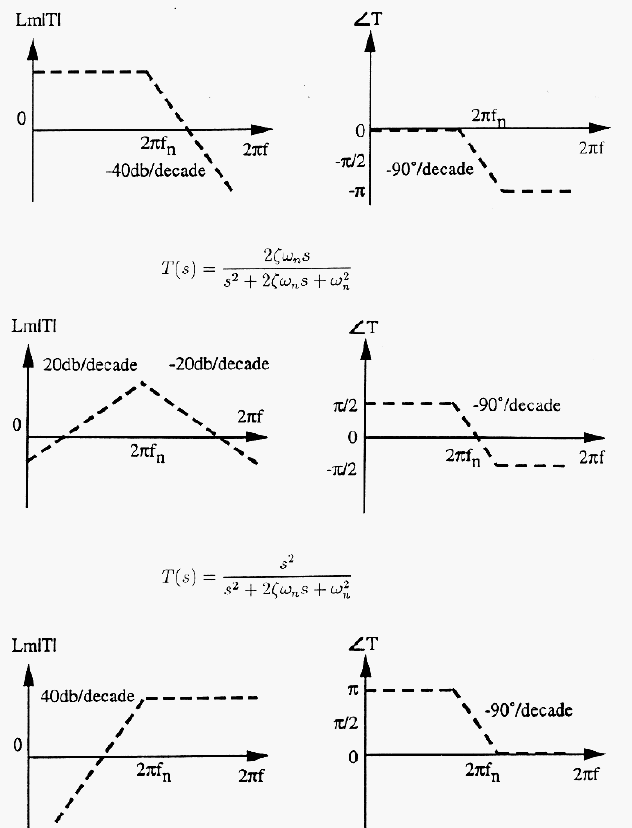
In the following plots,





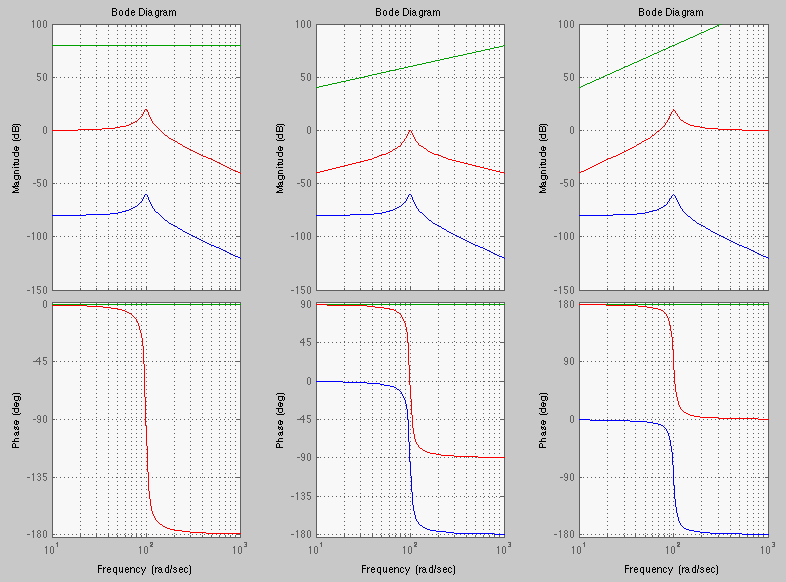
Example, a Band-pass filter:
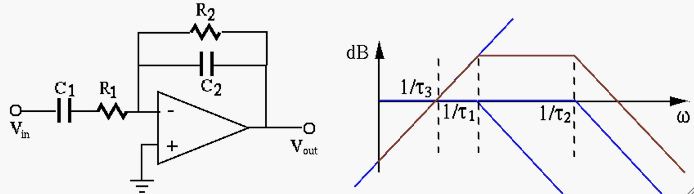
 |
(543) |
 ,
,
 ,
,
 .
.