Load/Source Matching for Maximum Power

Maximize power delivery in AC systems

Previously we considered the maximization of the power received by a resistive load $R_L$. This problem can be generalized to AC circuit containing $C$ and $L$, as well as $R$. Consider a voltage source composed of an ideal voltage source $\dot{V}_0=V_{rms}\angle 0^\circ$ in series with an internal impedance $Z_0=R_0+jX_0$, and a load impedance $Z_L=R_L+jX_L$. The load current is:

$$\dot{I}=\frac{\dot{V}_0}{Z_0+Z_L}=\frac{\dot{V}_0}{(R_0+R_L)+j(X_0+X_L)}$$ (411)

And we have:

$$\vert\dot{I}\vert^2=I^2_{rms}=\frac{\vert\dot{V}_0\vert^2}{\vert Z_0+Z_L\vert^2} =\frac{V^2_{rms}}{(R_0+R_L)^2+(X_0+X_L)^2}$$ (412)

The real power consumed by the load is:

$$P_L=I_{rms}^2 R_L =\frac{V^2_{rms}R_L}{(R_0+R_L)^2+(X_0+X_L)^2} =\frac{V^2_{rms}R_L}{\vert Z_0+Z_L\vert^2}$$ (413)

The denominator is the squared magnitude of a complex variable $Z_0+Z_L=(R_0+R_L)+j(X_0+X_L)$, which is minimized if the imaginary part $X_0+X_L$ is zero, i.e., $X_0=-X_L$ (while the real part $R_0+R_L>0$ is always positive). Now $P_L$ becomes:

$$P_L=I_{rms}^2 R_L=\frac{V^2_{rms}R_L}{(R_0+R_L)^2}$$ (414)

This is the power delivered to the load resistance $R_L$, which is maximized if it matches the internal resistance of the source $R_L=R_0$, as discussed before. Combining these two requirements $X_L=-X_0$ and $R_L=R_0$, we conclude that if $Z_L=R_L+jX_l=R_0-jX_0=Z_0$, i.e., the load impedance $Z_L$ is the complex conjugate of the internal impedance $Z_0$, the load receives maximum power:

$$P_L=\frac{V^2_{rms}R_L}{(R_0+R_L)^2}=\frac{V_{rms}^2}{4R_0}$$ (415)

Example 1:

Find load impedance $Z_L$ so that it receives maximum power from the rest of the circuit. Find this maximum power $P_L$ and load current $\dot{I}_L$.

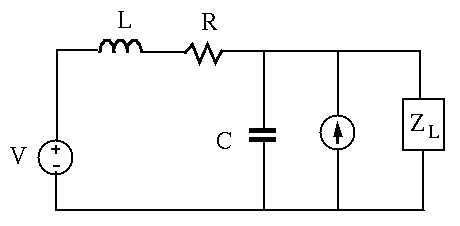
Assume voltage source $V_0=200 V$, current source $I_0=j\;10 A$, and the impedances of $R$, $L$, and $C$ are respectively $10\;\Omega$, $j\;10\;\Omega$, and $-j\;10\;\Omega$. To solve this circuit, we can use either Thevenin's voltage source or Norton's current source method.

• Find $Z_N=Z_T$: turn off both voltage and current sources, find $Z_{RL}=Z_L+Z_R=10+j10$ and the internal (Thevenin or Norton) impedance:

  $$Z_N=Z_T=Z_{RL}\vert\vert Z_C=\frac{Z_{RC}Z_C}{Z_{RC}+Z_C} =\frac{-j10(10+j10)}{10+j10-j10}=10(1-j)=R_0+jX_0$$ (416)

  where $R_0=10\;\Omega$, $X_0=-10\;\Omega$.
• Find open-circuit voltage $\dot{V}_T=\dot{V}_{oc}$ across load port by superposition principle. Due to voltage source alone:

  $$\dot{V}'_{oc}=V_0\frac{Z_C}{Z_{RL}+Z_C} =200\frac{-j10}{(10+j10)-j10}=-200j$$ (417)

  Due to current source alone:

  $$\dot{V}''_{oc}=I_0\;Z_{RL}\vert\vert Z_C =j10\frac{(10+j10)(-j10)}{(10+j10)-j10}=100+100j$$ (418)

  Now we have

  $$\dot{V}_T=\dot{V}_{oc}=\dot{V}'_{oc}+\dot{V}''_{oc}=-200j+100+100j=100(1-j) =100\sqrt{2}\angle(-45^\circ)$$ (419)

• Find short-circuit current $\dot{I}_N=\dot{I}_{sc}$ through load port by superposition principle:

  $$\dot{I}_N=I_0+\frac{V_0}{Z_{RL}} =10j+\frac{200}{10+10j}=10j+\frac{20(1-j)}{(1+j)(1-j)}=10$$ (420)

The relationship between the Norton current and Thevenin voltage can be verified:

$$\dot{I}_N Z_N=10\times10(1-j)=100(1-j)=100\sqrt{2}\angle(-45^\circ)=\dot{V}_T$$ (421)

For the load to receive maximum power, it needs to be

$$Z_L=Z_T=Z_N=R_0-jX_0=10(1+j)$$ (422)

The maximum power delivered to load is:

$$P_L=\frac{V^2_{rms}}{4R_0}=\frac{(100\sqrt{2})^2}{4\times 10}=500\;W$$ (423)

The current through the load is:

$$\dot{I}=\frac{\dot{V}}{2R_0}=\frac{100\sqrt{2}\angle(-45^\circ)}{20} =5\sqrt{2}\angle (-45^\circ)$$ (424)

Geometric mean method

The load resistance $R_L$ will receive maximum power only if it matches the internal resistance $R_0$ of the voltage source, $R_L=R_0$. However, when $R_L\ne R_0$, the resistance match can still be achieved by inserting a matching circuit between the source and load as shown in the figure.

The matching circuit is composed of two capacitors $C_1=C_2$ of the same impedance $-jX$ and an inductor $L$ of impedance $jX$. Alternatively, the two capacitors and the inductor in the matching circuit can be replaced by two inductors and a capacitor. If the frequency of the voltage source is $\omega=2\pi f$, then $X=\omega L=1/\omega C$, i.e., $LC=1/\omega^2$.

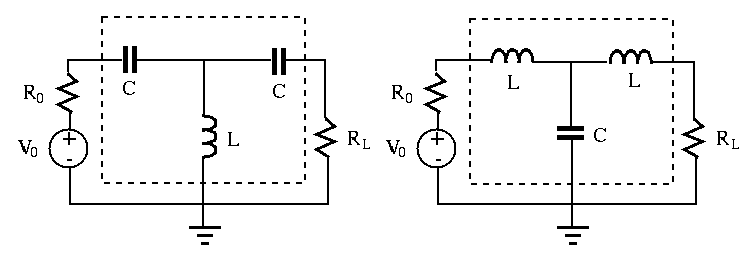
The total impedance of the new load composed of all four components $C_1=C_2$, $L$ as well as $R_L$ is real (resistive):

$$Z_L=-jX+jX \vert\vert (R_L-jX)=-jX+\frac{jX(R_L-jX)}{R_L}=\frac{X^2}{R_L}$$ (425)

Or, in the alternative case, the impedance of the new load is the same:

$$Z_L=jX+(-jX) \vert\vert (R_L+jX)=jX+\frac{-jX(R_L+jX)}{R_L}=\frac{X^2}{R_L}$$ (426)

For this load impedance $Z_L$ to match the internal resistance $R_0$ of the source, we have

$$Z_L=\frac{X^2}{R_L}=R_0,\;\;\;\;\;\; \;\;\;\;\;\;\;X=\sqrt{R_0R_L}$$ (427)

i.e., the reactance $X$ is the geometric mean of the source and load resistances $R_0$ and $R_L$. Note that the matching circuit consumes no real power as it does not have any resistance. We can verify that the power consumed by $R_L$ is $P_L=V^2/4R_0$.

This method can be generalized to any AC circuit composed of a voltage source with an internal impedance $Z_0=R_0+jX_0$ and load impedance $Z_L=R_L+jX_L$ in the following two steps:

• Replace the impedance $-jX$ of capacitor $C_1$ in series with the source by $-j(X+X_0)$, so that the additional reactance $-jX_0$ cancels the source reactance $X_0$, and the impedance in the source branch is $R_0-jX$.
• Replace the impedance $-jX$ of capacitor $C_2$ in series with the load by $-j(X+X_L)$, so that the additional reactance $-X_L$ cancels the load reactance $X_L$, and the impedance in the load branch is $R_L-jX$.

We can show that the impedance of the equivalent load composed of $-j(X+X_0)$, $jX$, and $-j(X+X_L)$ of the matching circuit and $Z_L=R_L+jX_L$ of the load is indeed the complex conjugate of the internal impedance $Z_L=R_0+jX_0$ of the source:

$$Z_L = -j(X+X_0)+jX \vert\vert (R_L-jX)=-j(X+X_0)+\frac{jX(R_L-jX)}{R_L}$$

$$= \frac{X^2}{R_L}-jX_0=R_0-jX_0 =Z_0$$ (428)

i.e., the load-source resistance match is achieved.

As this method requires a fixed reactance $X$, it is valid for single frequency $\omega=1/\sqrt{LC}$.

Example 2:

An audio amplification circuit with an output voltage $V_0$ and internal resistance $R_0=200\;\Omega$ is used to drive a speaker with $R_L=8\;\Omega$. The power received by the speaker is:

$$P_L=I^2R_L=\frac{V_0^2}{(R_0+R_L)^2}R_L=V_0^2\frac{8}{208^2}$$ (429)

The power consumed by the internal resistance $R_0$ is:

$$P_0=I^2R_0=\frac{V_0^2}{(R_0+R_L)^2}R_0=V_0^2\frac{200}{208^2}$$ (430)

The total power delivered is:

$$P_T=P_L+P_0=\frac{V_0^2}{R_0 \vert\vert R_L} =V_0^2\frac{208}{208^2}$$ (431)

The speaker gets only $P_L/P_T=8/208=3.8\%$ of the total power, while the remaining $P_0/P_T=200/208=96.2\%$ of the power is consumed internally.

To maximize the power delivered to the speaker, we add a matching circuit composed of $C_1=C_2$ with impedance $Z_C=-jX$ and $L$ with impedance $X_L=jX$. When $X=\sqrt{R_0R_L}=\sqrt{1600}=40$, the resistance of the new load $R'_L=200\;\Omega$ matches the internal resistance $R_0$ of the source, and the speaker receives maximum power of $P_L=V_0^2/4R_0=V^2/800$ (half of the total power $P_T=V^2/2R_0=V^2/400$), 6.76 times the power without the matching circuit.

As the frequency in the system is not constant, the matching is achieved only at one particular frequency, typically chosen to be the middle of the frequency range.

Matching resistances by a transformer

An ideal transformer can be used to match the load $R_L$ to the internal resistance $R_0$ of the source. Recall the following relations for an i deal transformer

$$P_1=V_1I_1=P_2=V_2I_2,\;\;\;\; \;\;\;\; \frac{I_2}{I_1}=\frac{V_1}{V_2}=\frac{n_1}{n_2}=r$$ (432)

where $r=n_1/n_2$ is the turn ratio. As $V_2=V_1/r$ and $I_2=rI_1$, we have

$$R_L=\frac{V_2}{I_2}=\frac{V_1/r}{rI_1}=\frac{1}{r^2}\frac{V_1}{I_1} =\frac{R'_L}{r^2}$$ (433)

where we have defined $R'_L=V_1/I_1$, which is related to the real load by $R'_L=r^2 R_L$. For the load to receive maximum power $P_L=P'_L$, we need to match the equivalent load resistance $R'_L$ to $R_0$:

$$R_0=R'_L=r^2 R_L,\;\;\;\;\; \;\;\;\;\; r=\frac{n_1}{n_2}=\sqrt{\frac{R_0}{R_L}}$$ (434)

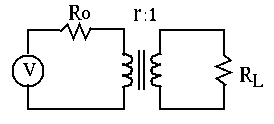
Example 3:

In the previous example with $R_0=200\;\Omega$, $R_L=8\;\Omega$, a transformer with turn ratio of $r=\sqrt{R_0/R_L}=\sqrt{200/8}=5$ can be used to match the load $R_L=8$ to internal resistance $R_0=200$.

Example 4:

$R_0=1000\Omega$, $R_L=10\Omega$, and the voltage source is $V=12V$. Find the turn ratio of the transformer so that the load resistor will get maximum power from the voltage source.

The load resistor receives maximum power if its resistance matches the internal resistance of the voltage source.

• Convert load resistance on the secondary side $R_L=10\Omega$ to $R'_L=r^2\; R_L=10\; r^2$ on the primary side.
• Match $R'_L=10\;r^2$ to $R_0$, i.e., $10\; r^2=1000\Omega$
• Find turn ratio $r=n_1/n_2=10$.
• Find power consumption on $R'_L$:

  $$P=\frac{V}{4R'_L}=36/1000=0.036W$$ (435)

• The power consumed by real load $R_L$ is the same, due to ideal transformer.