Active Components and Circuits

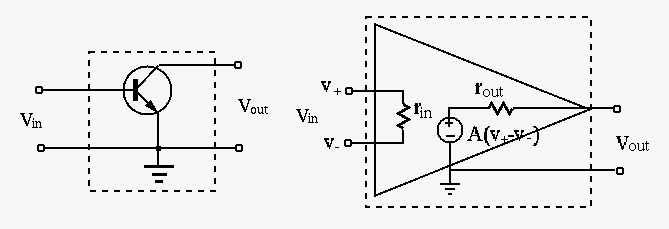
All circuits we have discussed so far are only composed of passive components (resistors, capacitors and inductors) driven by current and/or voltage sources. Later we will consider circuits containing active components such as bipolar junction transistors (BJT), field-effect transistors (FET), operational amplifiers (op-amps) containing many transistors, and voltage amplifiers. These active components can be considered as controlled voltage or current sources as functions (typically linear) of the input voltage or current.

We first consider modeling the overall function and performance of an active component (instead of its internal structure and implementation which may be very complicated) by the following three parameters:
- Input impedance (resistance) $r_{in}$ : It is desirable to have a large $r_{in}$ so that little input current is drawn from the source, i.e., the source is minimally affected by the amplifier as a load. Ideally $r_{in}=\infty$ .
- Output impedance (resistance) $r_{out}$ : It is desirable to have a small $r_{out}$ so that little voltage drop across this resistance will result when the load of the amplifier draws a current from the amplifier, i.e., the load will minimally affect the output voltage of the amplifier.
- Voltage gain (or in op-amp): The open-circuit voltage $v_{out}$ across the output port is related to the input voltage $v_{in}$ by $v_{out}=G_v v_{in}$ .
- Current gain (or $\beta$ in BJT transistor): The short-circuit current $i_{out}$ through the output port is related to the input current $i_{in}$ by $i_{out}=G_a i_{in}$ .
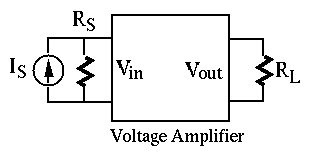
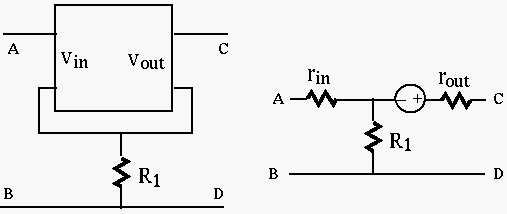
Example 1: Consider the circuit below containing an active component, a voltage amplifier, model by the three parameters $r_{in}$ , $r_{out}$ and , driven by either a current source or a voltage with internal resistance :

$\displaystyle v_{in}=i_s (R_S \,\vert\vert\, r_{in})=i_s \frac{R_S\; r_{in}}{R_S+r_{in}} =v_s \frac{r_{in}}{R_S+r_{in}}$ (133)

$\displaystyle v_{out}=G_v v_{in} \frac{R_L}{R_L+r_{out}} =G_v i_s \frac{R_S \;r... ...ac{R_L}{R_L+r_{out}} =G_v v_s \frac{r_{in}}{R_S+r_{in}} \frac{R_L}{R_L+r_{out}}$ (134)

Given and , we want to maximize $v_{out}$ by maximizing $r_{in}$ and minimizing $r_{out}$ .
We next consider a circuit containing an active circuit such as a transistor, an op-amp, or a voltage amplifier. This circuit can be modeled as a two-port network with input port between terminals A and B and output port between terminals C and D, and described in terms of the three parameters, the open-circuit voltage gain, the input resistance and output resistance:
- Input resistance $R_{in}$ : This is the resistance between the two terminals A and B of the input port, while a load is connected to the output port between terminals C and D:
  
  $\displaystyle R_{in}=\frac{\mbox{voltage $v_{in}$\ across the input port}} {\mbox{current $i_{in}$\ through the input port}}$ (135)
  
  In general $R_{in}$ is affected by the load .
- Output resistance $R_{out}$ : According to Thevenin's theorem, any one-port network can be treated as an ideal voltage source in series with a resistance . We apply this theorem to the output port and define the output resistance as the Thevenin resistance
  
  $\displaystyle R_{out}=\frac{\mbox{open-circuit voltage}}{\mbox{short-circuit current}} =\frac{v_{oc}=v_T\;\;(R_L=\infty)}{i_{sc}=v_T/R_T\;\;(R_L=0)}=R_T$ (136)
  
  while a voltage source with an internal resistance is applied to the input port. In general, $R_{out}$ is affected by of the source.
- The open-circuit voltage gain $A_{oc}$ : This is the ratio of the open-circuit output voltage $v_{oc}$ ( $R_L=\infty$ ) to an ideal voltage source
  
  $\displaystyle A_{oc}=\frac{\mbox{open-circuit voltage}}{\mbox{ideal voltage source}} =\frac{v_{oc}}{v_{in}}$ (137)

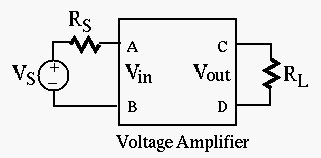
Example 2:

Find $R_{in}$ , $R_{out}$ , and $A_{oc}$ of this two-port network containing $R_1$ and $R_2$ as well as the amplifier modeled by $r_{in}$ , $r_{out}$ and the open-circuit voltage gain $G_v$ .

Input resistance: By inspection, the input resistance of this 2-port network can be found to be $R_{in}=R_1+r_{in}$ .
Output resistance: We assume the internal voltage source is the Thevenin voltage , and get the open-circuit voltage $v_{oc}=v_T R_2/(r_{out}+R_2)$ and the short-circuit current $i_{sc}=v_T/r_{out}$ . The output resistance is

$\displaystyle R_{out}=\frac{v_{oc}}{i_{sc}}=\frac{r_{out}R_2}{r_{out}+R_2}=r_{out}\,\vert\vert\,R_2$ (138)

Alternatively, $R_{out}$ can be found as the resistance between the two terminals C and D of the output port when the voltage source of the amplifier is turned off (short-circuit), i.e., $R_{out}=r_{out}\,\vert\vert\,R_2$ .
Open-circuit voltage gain: This is the ratio of the voltage $V_{CD}$ across the output port to the voltage $V_{AB}$ across the input port, when the output port is an open circuit, i.e., $R_L=\infty$ .

$\displaystyle v_{in}$ $\displaystyle =$ $\displaystyle V_{AB}\frac{r_{in}}{R_1+r_{in}}$

$\displaystyle V_{CD}$ $\displaystyle =$ $\displaystyle A v_{in} \frac{R_2}{r_{out}+R_2}=A V_{AB}\frac{r_{in}}{R_1+r_{in}} \frac{R_2}{r_{out}+R_2}$

$\displaystyle A_{oc}$ $\displaystyle =$ $\displaystyle \frac{V_{CD}}{V_{AB}}=\frac{A R_2 r_{in}}{(R_1+r_{in})(r_{out}+R_2)} \stackrel{r_{in}\rightarrow\infty\;\;r_{out}=0}{\Longrightarrow}A$ (139)

This 2-port network modeled as a voltage amplifier with $R_{in}$ , $R_{out}$ and $A_{oc}$ can be used in more complicated circuits.

Example 3:

A 2-port network with a voltage aplifier modeled by $r_{in}$ , $r_{out}$ and voltage gain $A$ on the left can be modeled by the circuit on the right. Find the parameters $R_{in}$ , $R_{out}$ and $A_{oc}$ of the two-port network with the voltage amplifier embedded.

Open-circuit voltage gain: As the output port is open circuit, the output current is zero and so is the voltage drop across $r_{out}$ . Applying an ideal voltage source to the input, we get the voltage $v_{in}$ across $r_{in}$ and across , respectively:

$\displaystyle v_{in}=v_s \frac{r_{in}}{R_1+r_{in}},\;\;\;\;\; v_1=v_s \frac{R_1}{R_1+r_{in}}$ (140)

The open-circuit voltage across output port is therefore:

$\displaystyle v_{oc}=v_1+A v_{in}=v_s \frac{R_1}{R_1+r_{in}}+Av_s\frac{r_{in}}{R_1+r_{in}} =v_s \frac{R_1+A r_{in}}{R_1+r_{in}}$ (141)

The open-circuit voltage gain can be found as the ratio of the open-circuit output voltage to the input voltage:

$\displaystyle A_{oc}=\frac{v_{oc}}{v_s}=\frac{R_1+A r_{in}}{R_1+r_{in}}<A$ (142)

if , the circuit is reduced to the original voltage amplifier and we have $A_{oc}=A$ .
Output resistance:
We first find the short-circuit current $i_{sc}$ at the output port. Assume a voltage source with internal resistance is applied to the input port while the output port is short-circuited. Applying KVL to the two loops of the circuit, we get:

$\displaystyle v_s=(R_S+R_1+r_{in})i_{in}-R_1 i_{sc}$ (143)

$\displaystyle A v_{in}=A r_{in} i_{in}=(r_{out}+R_1) i_{sc}-R_1 i_{in}$ (144)

Solving these two equations for the two unknowns $i_{in}$ and $i_{sc}$ , we get

$\displaystyle i_{sc}=v_s \frac{Ar_{in}+R_1}{(1-A)R_1 r_{in} +r_{out}(R_S+r_{in}+R_1)+R_SR_1}$ (145)

The open-circuit output voltage $v_{oc}$ is

$\displaystyle v_{oc}=Ar_{in}i_{in}+R_1i_{in}=(Ar_{in}+R_1)\frac{v_s}{R_S+r_{in}+R_1}$ (146)

Now the output resistance can be found to be:

$\displaystyle R_{out}=\frac{v_{oc}}{i_{sc}} =\frac{(1-A)r_{in}R_1+r_{out}(R_S+r... ...R_SR_1}{R_S+r_{in}+R_1} =r_{out}+\frac{(1-A) r_{in}R_1 +R_SR_1}{R_1+r_{in}+R_S}$ (147)

Note that $R_{out}$ is affected by internal resistance of the source. When ,

$\displaystyle R_{out}\stackrel{R_S=0}{\Longrightarrow} r_{out}-(A-1) r_{in}\,\vert\vert\,R_1 < r_{out}$ (148)

i.e., the output resistance is much reduced. Moreover, when , $R_{out}=r_{out}$ .
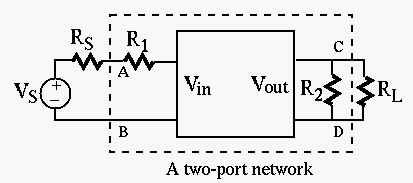
Input resistance: This can be found by applying an ideal voltage source to the input port, while the output port is connected to a load . The input resistance is $R_{in}=v_s/i_{in}$ where $i_{in}$ is the input current. Applying the KVL to the two loops of this circuit, we get

$\displaystyle v_s=(r_{in}+R_1) i_{in}-R_1 i_{out}$ (149)

$\displaystyle A v_{in}=Ar_{in}i_{in}=(r_{out}+R_L+R_1)i_{out}-R_1i_{in}$ (150)

Solving these two equations for the two unknowns $i_{in}$ and $i_{out}$ , we get

$\displaystyle i_{in}=v_s \frac{R_1+R_L+r_{out}}{(R_L+r_{out})(R_1+r_{in})+(1-A)... ..._{in}} \stackrel{R_L\rightarrow \infty}{\Longrightarrow} \frac{v_s}{r_{in}+R_1}$ (151)

Now the input resistance can be found to be

$\displaystyle R_{in}=\frac{v_s}{i_{in}}=\frac{(R_L+r_{out})(R_1+r_{in})+(1-A)R_... ..._L+r_{out}} \stackrel{R_L\rightarrow \infty}{\Longrightarrow} R_1+r_{in}>r_{in}$ (152)

Note that $R_{in}$ is affected by the load . When $R_L=\infty$ , $R_{in}=R_1+r_{in}$ , i.e., the input resistance is much increased. Moreover, if , the circuit is reduced to the original voltage amplifier with $R_{in}=r_{in}$ .

In summary, the resistor $R_1$

shared by both the input and output loops serves as a negative feedback:

$\displaystyle v_s\uparrow \rightarrow i_{in}, v_{out}\uparrow \rightarrow v_1\uparrow \rightarrow i_{in}, v_{out}\downarrow$

(153)

As the result, the voltage gain $A_{oc}$ is reduced but both the input and output resistances are improved, i.e., $R_{in}$ is increased and the $R_{out}$ is reduced.

Example 4: (Homework)

The transistor emitter follower and the op-amp buffer shown below are very important circuits which find wide applications in practice. These two circuits can be similarly modeled based on the individual models of the transistor and the an op-amp (the inner dashed boxes), also shown in the figure. Note that the two models are equivalent (the outter dashed boxes), as the non-ideal current and voltage in the models can be converted to each other.

The parameter $\beta$ of the transistor model is its current gain, and the parameter $A$ of the op-amp model is its voltage gain, both of them are much greater than 1. And for the op-amp, we also have $r_{in}>>r_{out}$ .

We can now find the three parameters of the model of the two circuits:

The input resistance $R_{in}=V_s/i_{in}$ , where is the source voltage applied across A and B, $i_{in}$ is the current through the input port, when a load is connected to the output port between C and D.
The output resistance $R_{out}=v_{oc}/i_{sc}$ , where $v_{oc}$ and $i_{sc}$ are the open-circuit voltage and short-circuit current when an ideal source voltage (with ) is applied to the input port.
The open-circuit gain $A_{oc}=V_{oc}/V_{sc}$ .

Answer

Example 5: (Homework)

Two amplifiers with parameters $A_1$ , $r_{i1}$ , $r_{o1}$ and $A_2$ , $r_{i2}$ , $r_{o2}$ , respectively, can be connected in cascade as shown in the figure. Given a voltage source $v_s$ in series with an internal resistance $R_S$ , find the output voltage. To maximize the output $v_{out}$ , how would you change the values of the six parameters?

Find the power gain $G_p$ of the system.

Answer

Example 6: (Homework)

The input and output resistances $R_{in}$ and $R_{out}$ , as well as the voltage gain $A_{oc}$ of a two-port network can be obtained experimentally. First, connect an ideal voltage source $v_s$ (a new battery with very low internal resistance) in series with a resistor $R_S$ , and then connect load $R_L$ of two different resistances to the output port. Now the three parameters can be derived from the known values of $v_s$ , $R_S$ and the two measurements of the load voltage $v_{out}$ , corresponding to the two resistance values used.

Assume $v_s=1.5V$ , $R_S=5 k\Omega$ , and the input voltage is measured to be $v_{in}=1.25 V$ ; also, assume the two different load resistors used are $R_1=150 \Omega$ and $R_2=200 \Omega$ respectively, with the two corresponding output voltage $v_1=18.75V$ and $v_2=20$ . Find $R_{in}$ , $R_{out}$ and $A_{oc}$ .

Answer

$\displaystyle v_{in}$	$\displaystyle =$	$\displaystyle V_{AB}\frac{r_{in}}{R_1+r_{in}}$
$\displaystyle V_{CD}$	$\displaystyle =$	$\displaystyle A v_{in} \frac{R_2}{r_{out}+R_2}=A V_{AB}\frac{r_{in}}{R_1+r_{in}} \frac{R_2}{r_{out}+R_2}$
$\displaystyle A_{oc}$	$\displaystyle =$	$\displaystyle \frac{V_{CD}}{V_{AB}}=\frac{A R_2 r_{in}}{(R_1+r_{in})(r_{out}+R_2)} \stackrel{r_{in}\rightarrow\infty\;\;r_{out}=0}{\Longrightarrow}A$	(139)