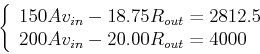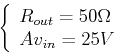The input and output resistances ![]() and
and ![]() , as well as the voltage
gain
, as well as the voltage
gain ![]() of a two-port network can be obtained experimentally. First,
connect an ideal voltage source
of a two-port network can be obtained experimentally. First,
connect an ideal voltage source ![]() (a new battary with very low internal
resistance) in series with a resistor
(a new battary with very low internal
resistance) in series with a resistor ![]() , and then connect load
, and then connect load ![]() of
two different resistances to the output port. Now the three parameters can
be derived from the known values of
of
two different resistances to the output port. Now the three parameters can
be derived from the known values of ![]() ,
, ![]() and the two measurements of
the load voltage
and the two measurements of
the load voltage ![]() , corresponding to the two resistance values used.
, corresponding to the two resistance values used.
Assume ![]() ,
, ![]() , and the input voltage is measured to be
, and the input voltage is measured to be
![]() ; also, assume the two different load resistors used are
; also, assume the two different load resistors used are
![]() and
and
![]() respectively, with the two corresponding
output voltage
respectively, with the two corresponding
output voltage ![]() and
and ![]() . Find
. Find ![]() ,
, ![]() and
and ![]() .
.
Solution:
First consider the voltage ![]() of the input port:
of the input port:
Next consider the voltage of the output port: