Energy Sources

Ideal Energy Sources:

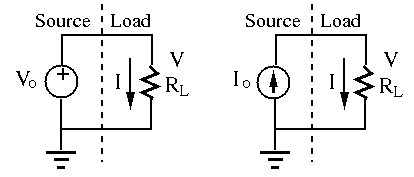
Consider the following ideal voltage source $V_0$ and ideal current source $I_0$, both directly connected to a load resistor $R_L$. We want to find both the load voltage $V$ across $R_L$ and the load current $I$ through $R_L$:

• An ideal voltage source provides constant voltage $V_0$ independent of the current through it $I=V_0/R_L$. The ideal voltage source can provide constant voltage to any number of resistors in parallel with the source, independent of how much current they each draw.

• An ideal current source provides constant current $I_0$ independent of the voltage across it $V=I_0 R_L$. The ideal current source can provide constant current to any number of resistors in series with the source.

However, such ideal sources do not exist in reality, due to the following dilemmas:

• If $R_L=0$ (short circuit), the load voltage $V=R_L I=0\ne V_0$,
• If $R_L=\infty$ (open circuit), the load current $I=V/R_L=V/\infty=0\ne I_0$,

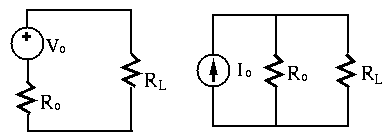
Realistic voltage source:

In reality, all voltage sources (e.g., a battery or a voltage amplifier circuit) can be more realistically modeled by an ideal voltage source $V_0$ in series with a nonzero internal resistance $R_0$, which causes an internal voltage drop $IR_0$ due to the current $I$ drawn by the load $R_L$, so that the actual output voltage across the load $V=V_0-IR_0< V_0$ is lower than $V_0$. The load voltage $V$ and current $I$ are constrained by the following two relationships imposed by the voltage source $(V_0, R_0)$ and the load $R_L$:

$$\left\{ \begin{array}{lll} \mbox{Source:} & V=V_0-IR_0\;\;\;\;\;\... ...,\;\;\;\;\;\;\;(V=0,\;\;I=V_0/R_0)\\ \mbox{load:} & V=R_LI \end{array} \right.$$ (101)

Solving for $I$ and $V$, we get:

$$\left\{ \begin{array}{l} I=V_0/(R_0+R_L) \\ V=R_L I=V_0\,R_L/(R_0+R_L) \end{array} \right.$$ (102)

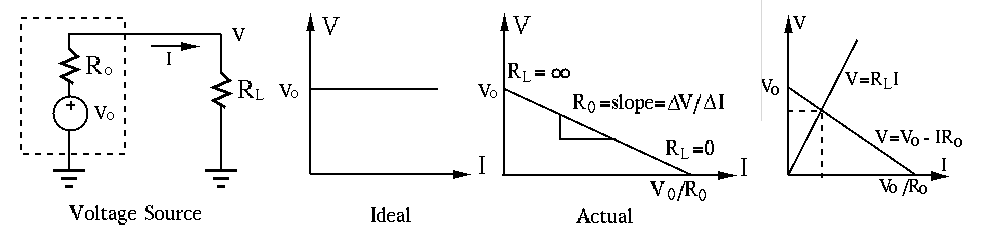
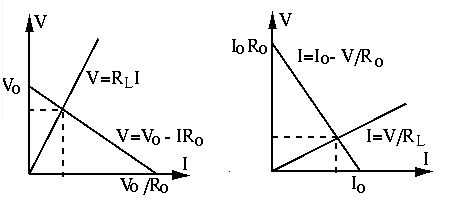
In the V-I plot, the function curve $V=V_0-IR_0$ for the voltage source intersects with the axes at two points: (1) the open-circuit voltage $V=V_0$ when $R_L=\infty$ and therefore $I=0$, and (2) the short-circuit current $I=V_0/R_0$ when $R_L=0$ and therefore $V=0$. The slope of the curve is the internal resistance $R_0$ of the voltage source.

The function curve $V=RI$ for the load is simply the Ohm's law, with slope $R_L$. Solving these two equations we get load voltage $V$ and current $I$.

For the output (load) voltage $V$ to be as close to the voltage source $V_0$ as possible, the internal resistance $R_0$ of a voltage source needs to be as small as possible, ideally $R_0=0$.

Only in the case of an ideal voltage source with $R_0=0$ will $V=V_0$. For $R_0>0$, the heavier the load, i.e., the smaller $R_L$, the larger the load current $I$, and the lower the load voltage $V$:

$$R_L \downarrow \Longrightarrow I \uparrow \Longrightarrow R_0I \uparrow \Longrightarrow V \downarrow$$ (103)

In particular, when the load is a short circuit ($R_L=0$), the output voltage of a battery is zero (instead of the specified $V_0=1.5V$), as the voltage drop across the nonzero internal resistance $R_0$ is the same as $V_0$, i.e., the electric energy of the battery is consumed internally, with no energy delivered to external circuit.

Realistic current source:

In reality, all current sources (e.g., a solar cell or a current amplifier circuit) can be modeled by an ideal current source $I_0$ in parallel with a nonzero internal resistance $R_0$, which causes an internal current $V/R_0$ so that the actual output current through the load $I=I_0-V/R_0<I_0$ is lower than $I_0$. The load voltage $V$ and current $I$ are constrained by the following two relationships imposed by the current source $(I_0, R_0)$ and the load $R_L$:

$$\left\{ \begin{array}{ll} \mbox{Source:} & I=I_0-V/R_0\;\;\;\;\;\... ...0),\;\;\;\;\;\;\;(V=0,\;\;I=I_0) \\ \mbox{Load:} & I=V/R_L \end{array} \right.$$ (104)

Solving for $V$ and $I$, we get

$$\left\{ \begin{array}{l} V=I_0R_0R_L/(R_0+R_L)=I_0\;R_0\vert\vert R_L \\ I=V/R_L=I_0R_0/(R_0+R_L)\end{array} \right.$$ (105)

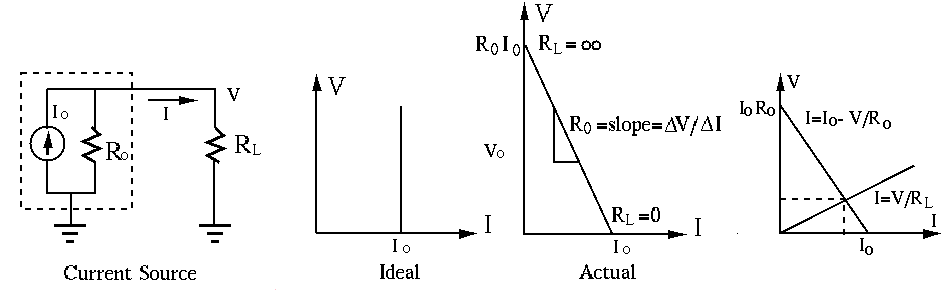
In the V-I plot, the function curve $V=I_0\;R_0R_L/(R_0+R_L)$ for the current source intersects with the axes at two points: (1) the open-circuit voltage $V=I_0R_0$ when $R_L=\infty$ and therefore $I=0$, and (2) the short-circuit current $I=I_0$ when $R_L=0$ and therefore $V=0$. The slope of the curve is the internal resistance $R_0$ of the current source.

The function curve $V=IR_L$ (i.e., $I=V/R_L$) for the load is simply the Ohm's law, with the slop $R_L$. Solving these two equations we get load voltage $V$ and current $I$.

The slope of the first curve is the internal resistance $R_0$ and the slope of the second curve is $R_L$. Solving these two equations we get load voltage $V$ and current $I$.

For the output (load) current $I$ to be as close to the current source $I_0$ as possible, the internal resistance $R_0$ of a current source should be as large as possible, ideally $R_0=\infty$.

Only in the case of an ideal current source will $R_0=\infty$ and $I=I_0$. For $R_0<\infty$, the larger the load resistance $R_L$, the smaller the current $I_L$.

$$R_L \uparrow \Longrightarrow V \uparrow \Longrightarrow V/R_0 \uparrow \Longrightarrow I \downarrow$$ (106)

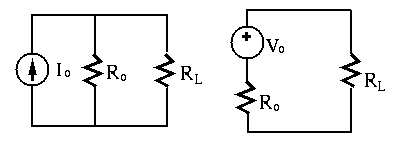
Energy Source Conversion

Any two circuits with the same voltage-current relation (V-I characteristics) at the output port with $R_L$ are equivalent to each other, as they have the same external behavior, although they may be different internally.

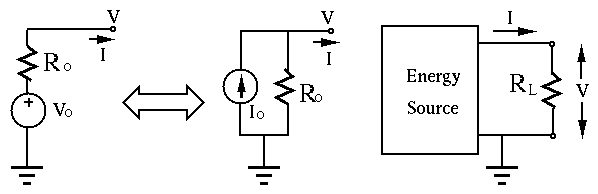
Comparing the voltage-current relations of the two energy sources:

• The voltage source ($V_0, R_0$):

  $$V=V_0-R_0I=R_0(V_0/R_0-I)$$ (107)

• The current source $(I_0, R'_0)$:

  $$V=R'_0(I_0-I)=R'_0I_0-R'_0I$$ (108)

If $R_0=R'_0$ and $V_0=I_0 R_0$, then the two sources have the same V-I characteristics and are therefore equivalent to each other. We also see that

• a non-ideal voltage source $(V_0, R_0)$ can be converted into a non-ideal current source $(I_0=V_0/R_0,\,R_0)$,
• a non-ideal current source $(I_0, R'_0)$ can be converted into a non-ideal voltage source $(V_0=I_0R'_0,\,R'_0)$.

Both of the two energy sources above can be treated as either a voltage or a current source.

• The source on the left has a small $R_0$ and is therefore a good voltage source as the voltage $V$ received by the load is close to the source voltage $V_0$, but a bad current source as the current $I$ received by the load is much lower than the source current $I_0=V_0/R_0$.
• The source on the right has a large $R_0$ and is therefore a bad voltage source as the voltage $V$ received by the load is much lower than the source voltage $V_0=I_0 R_0$, but a good current source as the current $I$ received by the load is close to the source current.

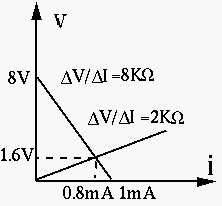
The Internal Resistance $R_0$:

The internal resistance $R_0$ can be found as the absolute value of the slope of the straight line of the V-I characteristic plot:

$$R_0=\frac{\vert\Delta V\vert}{\vert\Delta I\vert}$$ (109)

where $\Delta V$ and $\Delta I$ are respectively the difference in voltage and current between any two points along the line, which can be chosen arbitrarily. The most convenient choice would be the intersections of the straight line with the $V$ and $I$ axes:

$$\begin{array}{c\vert\vert c\vert c}\hline & \mbox{Open circui... ...rent Source} & V_{oc}=I_0R_0 & I_{sc}=I_0 \\ \hline \end{array}$$ (110)

In either case, we have:

$$\frac{\mbox{open-circuit voltage}}{\mbox{short-circuit current}} ... ...voltage source)}\\ (I_0R_0)/I_0&\mbox{(current source)}\end{array}\right\}=R_0$$ (111)

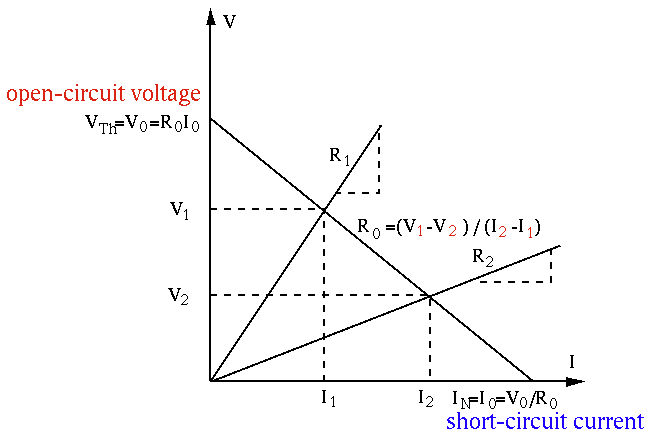
While this method can be used to find the internal resistance $R_0$ without knowing either $I_0$ or $V_0$ in theory, it may not be practical, as the short circuit current is difficult to get (the voltage source may be damaged). Instead, we can find some other two voltages and currents $V_i$ and $I_i$ ($i=1,2$) corresponding to two load resistors $R_1$ and $R_2$. Then $R_0$ can be found as the slope of the straight line determined by the two points $(V_1, I_1)$ and $(V_2, I_2)$. We see that the previous method can be considered as a special case when $R_1=\infty$ (open circuit) and $R_2=0$ (short circuit).

Example 1:

A given voltage source of $V_0=10V$ and $R_0=10\Omega$ can be converted to a current source of $I_0=V_0/R_0=1A$ with the same $R_0$ (and vice versa). A load of $R_L=40\Omega$ receives from this energy source a voltage $V_L=8V$ (80% of the voltage source) and a current $I_L=0.2A$ (20% of the current source). As the energy source has a low internal resistance $R_0$, it is a good voltage source but a poor current source.

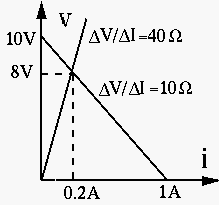
Example 2:

A given current source of $I_0=1 mA$ and $R_0=8 K\Omega$ can be converted to a voltage source of $V_0=I_0 R_0=8V$ with the same $R_0$ (and vice versa). A load of $R_L=2 K\Omega$ receives from this energy source a voltage $V_L=1.6V$ (20% of the voltage source) and a current $I_L=0.8 mA$ (80% of the current source). As energy source has a high internal resistance $R_0$, it is a good current source but a poor voltage source.

Power Delivery/Absorption

• Voltage source
  • If the direction of the current $I$ in a circuit is such that it goes internally through a voltage source $V$ from its low potential (-) to high (+), and externally through the rest of the circuit from high to low, then the polarities of the voltage and the current are consistent (both positive or negative depending on the assumed polarity), and the source is delivering power $W=VI$.
  • If the direction of the current is reversed, then the power delivered $W=-VI$ will be negative, i.e., the voltage source is actually receiving power. A typical example is the rechargeable battery in your car that works in either of the two states.
• Current source
  • If the polarity of the voltage $V$ across a current source is such that the head of the arrow of the current source is at high potential (+) and the tail of the arrow is at low potential (-), then the polarity of the voltage and the current is consistent, and the current source is delivering power $W=VI$.
  • If the direction of the current is reversed, then the power delivered $W=-VI$ will be negative, i.e., the current source is actually receiving power.

Example 3:

The current in a circuit composed of an ideal voltage source $V_0=5\,V$ and a resistor $R=5\Omega$ is $I=V/R=1\,A$. The power consumption of the resistor and voltage source are $W_R=I^2R=V^2/R=IV=5$ and $W_V=-IV=-5$, respectively. The negative value of $W_V$ indicates the power is actually not consumed but generated by the voltage source (converted from other forms of energy, e.g., chemical, mechanical, etc.)

Example 4:

In the circuit shown below, the ideal current source is $I_0=1A$, and the ideal voltage source is $V_0=2V$, the resistor is $R=3\Omega$. Find the current through and voltage across each of the three components. Find the power delivered, absorbed, or dissipated by each of the three components.

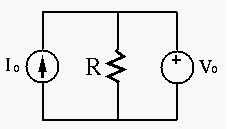
The current source provides $I_0=1A$ current through the left branch (upward), while the voltage source provides $V_0=2V$ across all three components. The current through $R$ is $2V/3\Omega=2/3A$ (downward), by KCL, the current through the voltage source is $I_v=1-2/3=1/3A$. We therefore have:

• Power dissipated by $R$ is $P_R=V_0^2/R=4/3\;W$,
• Power received by voltage source is $P=V_0I_V=2/3\;W$.
• Power delivered by current source is $P=V_0I_0=2\;W$ $(2/3+4/3=2)$.

(Homework) Redo the above with the polarity of $V_0$ reversed. Find:

• Power dissipated by $R$:
• Power received/delivered by voltage source:
• Power delivered/received by current source:

Verify your results so that total power delivered is equal to total power received and dissipated.

Answer

Comment: While various voltage sources such as batteries are common in everyday life, current sources do not seem to be widely available. One type of current source is solar-cell, which generates current proportional to the intensity of the incoming light. Also, certain transistor circuits are designed to output constant current. Moreover, as discussed above, any voltage source can be converted into a current source. For example, a current source with $I_0=1$ mA and $R_0=1\;M\Omega$ can be implemented by a voltage source of $V_0=1000\; V$ in series with $R_0=1\;M\Omega$.

Example 5 (Homework)

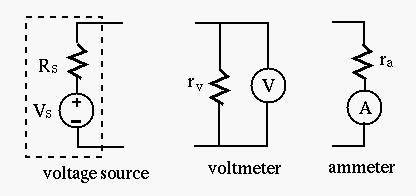
A realistic voltage source (e.g., a battery) can be modeled as an ideal voltage source $V_0$ in series with an internal resistance $R_0$. Ideally, the voltage $V_0$ can be obtained by measuring the open-circuit voltage $V_{oc}$ with a voltmeter

$$V_0=V_{oc}$$ (112)

while the internal resistance $R_0$ can be obtained as the ratio of the open-circuit voltage $V_{oc}$ to the shirt-circuit current $I_{sc}$, which can be measured by an ammeter:

$$R_0=\frac{V_{oc}}{I_{sc}}$$ (113)

However, in reality, any voltmeter has an internal resistance $R_v$ in parallel with the meter, and any ammeter has an internal resistance $R_a$ in series with the meter. For better measurement accuracy, should $R_v$ be small or large, how about $R_a$? Why? Give the expression of the measured open-circuit voltage $V$ and short-circuit current $I$ in terms of the true $R_0$ and $V_0$, as well as $R_v$ and $R_a$.

Assume $V_0=6V, R_0=100\Omega, R_v=10,000 \Omega, R_a=200 \Omega$. What are the measured open-circuit voltage $V$, and the short-circuit current $I$? Given $V$, $I$, and the known $R_v$ and $R_a$, how do your get the true $V_0$ and $R_0$ using your method above? Show your numerical computations.

Answer

Design a method to obtain the true source voltage $V_0$ and internal resistance $R_0$ by a voltmeter and an ammeter with known $R_v$ and $R_a$. Give the expression of $V_0$ and $R_0$ in terms of the measured open-circuit voltage $V$, short-circuit $I$, and $R_v$ and $R_a$.

Answer

Example 6 (Homework)

Usually the internal resistances of the voltmeter and ammeter are not readily known (and the values may change depending on the scale used). As another method to find $R_0$ and $V_0$ of a voltage source, we can measure the voltage $V_L$ across two different load resistors $R_L$ connected to the voltage source. If the values of $R_L$ are significantly smaller than that of the internal resistance $R_v$ of the voltmeter, the voltmeter can be considered to be ideal with $R_v\rightarrow \infty$.

Assume when the load resistor is $R_L=1 k\Omega$, the voltage across it is found to be $V_L=9.09V$, when a different load $R_L=2 k\Omega$ is used and the voltage across it is $V_L=9.52V$. Find $V_0$ and $R_0$ of the voltage source.

Answer:

$$V_0\frac{1}{R_0+1}=9.09,\;\;\;\;\;\;V_0\frac{2}{R_0+2}=9.52$$ (114)

i.e.,

$$V_0=9.09\,R_0+9.09,\;\;\;\;\;\;\;V_0=4.76\,R_0+9.52$$ (115)

Subtracting we get

$$R_0=\frac{9.52-9.09}{9.09-4.76}=\frac{0.43}{4.33}\approx 0.1\;k\Omega$$ (116)

and

$$V_0=9.09\,R_0+9.09=9.09\times 0.1+9.09=10\,V$$ (117)