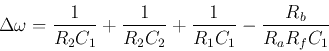Next: The Twin-T notch (band-stop)
Up: Chapter 6: Active Filter
Previous: First and Second Order
The
Sallen-Key filters
are second-order active filters (low-pass, high-pass, and band-pass) that
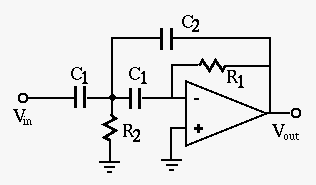
can be easily implemented using the configuration below:
We represent all voltages in phasor form. Due to the virtual ground
assumption,
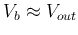 at non-inverting input is virtually
the same as that at the inverting input, which is connected to the
output
at non-inverting input is virtually
the same as that at the inverting input, which is connected to the
output 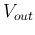 . Applying KCL to nodes a and b to get:
. Applying KCL to nodes a and b to get:
and
The second equation can also be written as
Substituting these into the first equation we get
Now the frequency response of the Sallen-Key filter can be found as
the ratio of 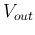 and
and 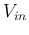 :
:
- Second order low-pass filter
If we let 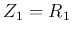 ,
, 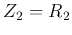 ,
,
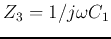 ,
,
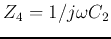 ,
then the FRF becomes:
,
then the FRF becomes:
This is a 2nd-order low-pass filter with
and
As there are only two parameters 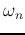 and
and 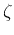 or
or 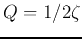 to satisfy, we can arbitrarily set any two of the four variables
to satisfy, we can arbitrarily set any two of the four variables 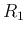 ,
,
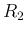 ,
, 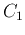 , and
, and 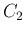 , and then solve for the other two. For example,
for convenience, if we let
, and then solve for the other two. For example,
for convenience, if we let 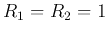 , we get
, we get
- Second order high-pass filter
If we let
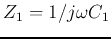 ,
,
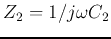 ,
, 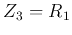 ,
, 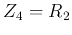 ,
then the FRF becomes becomes:
,
then the FRF becomes becomes:
This is a 2nd-order high-pass filter with
and
We further consider a band-pass filter shown below:
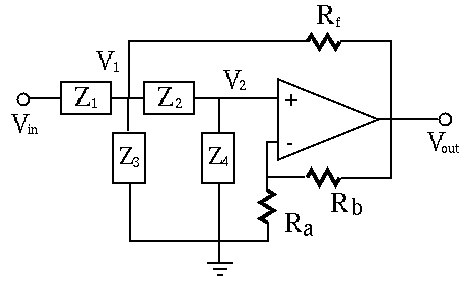
By voltage divider and virtual ground, we get
Apply KCL to node 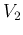 to get:
to get:
Apply KCL to node 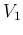 to get:
to get:
Rearrange the terms, and replace 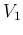 by
by
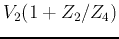 to get
to get
Further rearrange the terms and replace 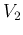 by
by 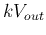 to get
to get
Further rearrange the terms
Finally we get the frequency response function:
If we let
the frequency response function becomes
This is a band-pass filter with the peak frequency equal to the natural
frequency:
the bandwidth
The gain of the filter is controlled by 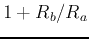 .
.
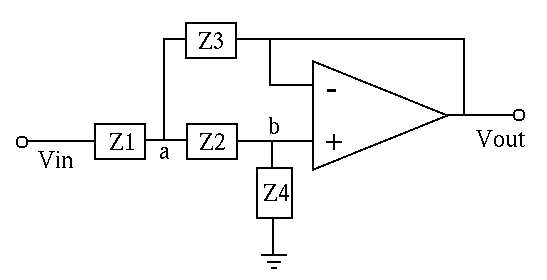
More Examples of op-amp filters are listed below
(with detailed analysis in here):



Next: The Twin-T notch (band-stop)
Up: Chapter 6: Active Filter
Previous: First and Second Order
Ruye Wang
2019-05-07


![]() at non-inverting input is virtually
the same as that at the inverting input, which is connected to the
output
at non-inverting input is virtually
the same as that at the inverting input, which is connected to the
output ![]() . Applying KCL to nodes a and b to get:
. Applying KCL to nodes a and b to get:
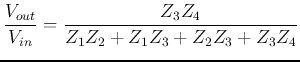
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
then the FRF becomes:
,
then the FRF becomes:
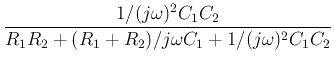
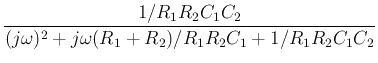
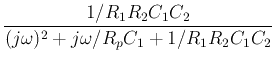
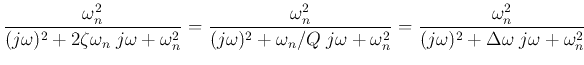
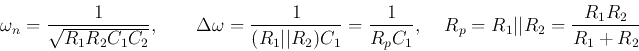
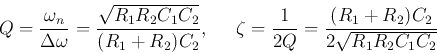
![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
then the FRF becomes becomes:
,
then the FRF becomes becomes:
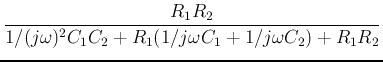
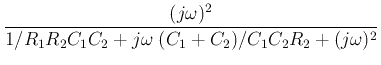
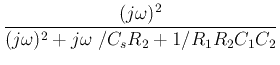
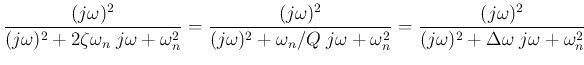
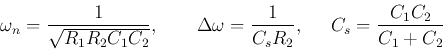
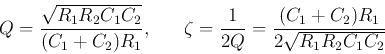

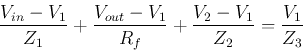
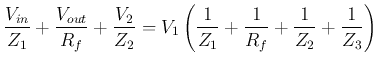
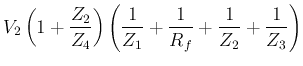
![\begin{displaymath}
\frac{V_{in}}{Z_1}+\frac{V_{out}}{R_f}
=kV_{out}\left[\lef...
..._f}
+\frac{1}{Z_2}+\frac{1}{Z_3}\right)-\frac{1}{Z_2}\right]
\end{displaymath}](img110.png)
![$\displaystyle kV_{out}\left[\left(1+\frac{Z_2}{Z_4}\right)
\left(\frac{1}{Z_1}
...
..._f}+\frac{1}{Z_2}+\frac{1}{Z_3}\right)-\frac{1}{Z_2}\right]-\frac{V_{out}}{R_f}$](img112.png)
![$\displaystyle V_{out}\left\{k\left[\left(1+\frac{Z_2}{Z_4}\right)\left(\frac{1}...
...}+\frac{1}{Z_2}+\frac{1}{Z_3}\right)-\frac{1}{Z_2}\right]-\frac{1}{R_f}\right\}$](img113.png)
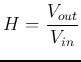
![$\displaystyle \frac{1}{Z_1\left\{k\left[\left(1+\frac{Z_2}{Z_4}\right)\left(\fr...
...+\frac{1}{Z_2}+\frac{1}{Z_3}\right)-\frac{1}{Z_2}\right]-\frac{1}{R_f}\right\}}$](img115.png)
![$\displaystyle \frac{1/k}{Z_1\left[\left(1+\frac{Z_2}{Z_4}\right)\left(\frac{1}{...
...{R_f}+\frac{1}{Z_2}+\frac{1}{Z_3}\right)-\frac{1}{Z_2}\right]-\frac{Z_1}{kR_f}}$](img116.png)