The Exam Problems (Don't click until you are ready)

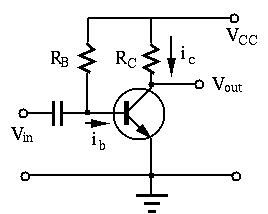
1. Problem 1. (30 points)

   In the transistor amplification circuit shown below, $V_{CC}=12V$, $\beta=100$. Assume the AC component of the input current is $i_b(t)=0.05\,\cos\omega t \;mA$. Sketch the output characteristic plot of the transistor circuit with the load line, and sketch the $i_C(t)$, output $v_C(t)$ on the same plot (similar to the output characteristic plot in the notes), and comment on both amplification and distortion for each of the following three cases:

   1. (10 pts) $R_B=110 K\Omega$, $R_C=1.2 K\Omega$;
   2. (10 pts) $R_B=110 K\Omega$, $R_C=0.6 K\Omega$;
   3. (10 pts) $R_B=220 K\Omega$, $R_C=1.2 K\Omega$.

   

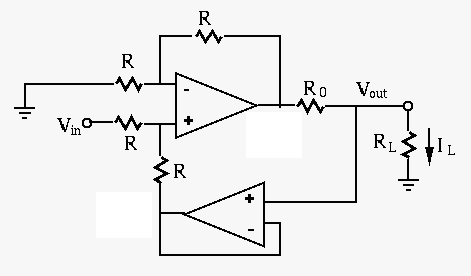
2. Problem 2 (30 points)

   Find the expression of the load current $I_L$ in terms of the input voltage $V_{in}$ and all relevant resistors in the circuit. Show that $I_L$ is independent of the load resistance $R_L$, i.e., this circuit can be used as a current source.

   (Hint: introduce an intermediate voltage $V$ at the output of the op-amp.)

   

3. Problem 3 (40 points)

   Given the op-amp circuit below:

   

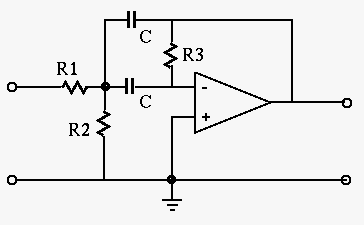
   1. (20 pts) Find its frequency response function (FRF) $H(\omega)=V_{out}/V_{in}$ in terms of $R_1,\;R_2,\;R_3$ and $C$. What kind of filter is this circuit?

   2. (20 pts) Given $C=10\,\mu F$, $R_1=8\,k\Omega,\; R_2=0.16\,k\Omega,\;R_3=16\,k\Omega$, find the frequency $\omega_0$ at which the magnitude of the FRF $\vert H(\omega)\vert$ reaches extreme (either maximum or minimum). If this is either a band-pass or band-stop filter, find the bandwidth $\Delta\omega$.