One-Sample t-Test

Given an observed data set $\{x_1,\cdots,x_N\}$ of $N$ i.i.d samples of a normal distribution ${\cal N}(x,\mu,\sigma^2)$ of unknown $\mu$ and $\sigma^2$, we can carry out the test of a null hypothesis $H_0$ claiming that the sample mean $\bar{x}$ is the same as an expected value such as a hypothesized mean $\mu_0$. As the result of the test, $H_0$ is either accepted or rejected in favor of one of the alternative hypotheses $H_a$:

• Null hypothesis $H_0$: $\mu=\mu_0$,
• Alternative hypothesis $H_A$:
  • $\mu\ne\mu_0$ (two-tailed)
  • $\mu>\mu_0$ (one-tailed-greater)
  • $\mu<\mu_0$ (two-tailed-smaller)

The one-sample t-test can be used to compare the mean of a population with an expected value, to see if there exists a significant difference. Examples include, the drinking water contaminants compared with standards/regulations, test scores of a school compared to the average of all schools in the district.

To test the null hypothesis $H_0$, we first find the sample mean

  $$\bar{x}=\frac{1}{N}\sum_{i=1}^N x_i \;\;\sim\;\; {\cal N}(\mu, \sigma^2/N)$$ (22)

and construct the following test statistic, assuming the variance $\sigma^2$ is known:

  $$z=\frac{\bar{x}-\mu_0}{\sigma/\sqrt{N}}=\frac{\bar{x}-\mu_0}{\mbox{SE}} \;\;\sim\;\;{\cal N}(z,0,1)$$ (23)

where $\mbox{SE}=\sigma/\sqrt{N}$ is the standard error.

If $\sigma^2$ is unknown (typically the case), we have to estimate it by the sample variance:

  $$S^2=\frac{1}{N-1}\sum_{i=1}^N (x_i-\bar{x})^2$$ (24)

and construct the test statistic with a t-distribution of $\nu=N-1$ degrees of freedom:

  $$t=\frac{\bar{x}-\mu_0}{S/\sqrt{N}}=\frac{\bar{x}-\mu_0}{\mbox{ESE}}\; \sim\;{\cal T}_{N-1}(t)$$ (25)

where $\mbox{ESE}=S/\sqrt{N}$ is the estimated standard error.

Evaluating $t$ based on the calculated $\bar{x}$ and $\mbox{ESE}=S/\sqrt{N}$, we get the specific value $t^*$ of the test statistic. Qualitatively, a larger value of $\vert t^*\vert$ indicates $\bar{x}$ and $\mu_0$ are more different, and $H_0$ for $\bar{x}=\mu_0$ is more likely to be rejected, in favor of an alternative hypothesis $H_a$, such as $\bar{x}\ne\mu_0$.

We also find the critical values $t_{\alpha/2}<0$ satisfying ${\cal T}_\nu(t_{\alpha/2})=\alpha/2$ and $t_{1-\alpha/2}=-t_{\alpha/2}>0$ satisfying ${\cal T}_\nu(t_{1-\alpha/2})=1-\alpha/2$, from the two-tailed t-Table of $\nu=N-1$, or the Matlab inverse cumulative density function icdf. For example, if $\alpha=0.05$ and $N=11$, i.e., $\nu=N-1=10$, we find $t_{\alpha/2}=-2.228$ and $t_{1-\alpha/2}=-t_{\alpha/2}=2.228$.

The probability for $t$ to fall inside the interval $[t_{\alpha/2},\;t_{1-\alpha/2}]$ is $1-\alpha$:

  $$P(t_{\alpha/2}<t<t_{1-\alpha/2})=1-\alpha$$ (26)

i.e., the probability for $t$ to fall inside the critical region outside the interval above is

  $$P( \vert t\vert > \vert t_{\alpha/2}\vert) = 1-P(t_{\alpha/2}<t<t_{1-\alpha/2}) =\alpha$$ (27)

We can now either accept or reject the null hypothesis $H_0$ for $\mu=\mu_0$, depending on whether $t^*$ falls inside the critical region:

• if $t^* < t_{\alpha/2}$, $t^*$ is in the critical region, indicating $\bar{x}$ is significantly smaller than $\mu_0$, $H_0$ is rejected;
• if $t^* > t_{1-\alpha/2}$, $t^*$ is in the critical region, indicating $\bar{x}$ is significantly greater than $\mu_0$, $H_0$ is rejected;
• if $t_{\alpha/2} < t^* < t_{1-\alpha/2}$, $t^*$ is not in the critical region, $H_0$ is not rejected.

Alternatively and equivalently, we can find the p-value based on the test statistic value $t^*$, from the t-Table or the Matlab cumulative density function cdf:

  $$p=P(\vert t\vert>\vert t^*\vert)=1-P(t<\vert t^*\vert)=1-\int_{-\vert t^*\vert}^{\vert t^*\vert} {\cal T}_\nu(\tau)\;d\tau$$ (28)

If $p<\alpha$, or equivalently, $\vert t^*\vert>\vert t_\alpha\vert$, then $t^*$ is inside the critical region, indicating the fact that observing this specific $t^*$ is a low probability event according to the null hypothesis $H_0$, but as it did happen, then the null hypothesis has to be rejected. On the other hand, if $p>\alpha$, the evidence against $H_0$ is not significant enough, i.e., rejecting $H_0$ has $p>\alpha$ chance of being wrong (but still $1-p$ chance of being right), we fail to reject $H_0$. However, this result is not necessarily a significant evidence for $H_0$.

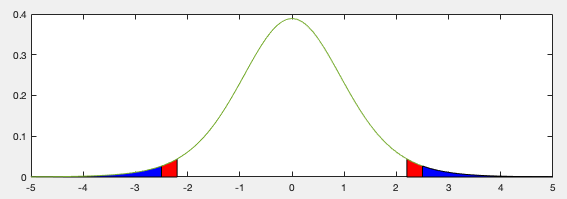
In the figure below, the one and two-tailed t-distributions of 10 d.f. are shown. In all cases, the red area is $\alpha=0.05$ determined by the critical value $t_\alpha$ in one-tailed case (top) or $t_{\alpha/2}$ in two-tailed case (bottom), the blank area underneath the pdf is $1-\alpha=0.95$, while the blue area is the p-value, determined by the value $t^*$ of the test statistic. In both cases,the null hypothesis is $\bar{x}=\mu_0$. If $p<\alpha$, $H_0$ is rejected, as data support the alternative hypothesis $H_a$, which is $\bar{x}>\mu_0$ in one-tailed case (top-left), or $\bar{x}\ne\mu_0$ in two-tailed case (bottom-left). If $p>\alpha$, $H_0$ is accepted (right).

In general, if $\bar{x}$ is very different from $\mu_0$ (strong signal), and the variance $\sigma^2$ or the sample variance $S$ is small and sample size $N$ is large (small noise), then the absolute value $\vert\bar{x}-\mu_0\vert/ESE$ of $t^*$ is large, and p-value is small, the null hypothesis is likely to be rejected.

If $\sigma^2$ is known, or if the sample size $N$ is large enough (e.g., $N>30$), then the test statistic $t=(\bar{x}-\mu_0)/ESE$ with t-distribution can be replaced by $z=(\bar{x}-\mu_0)/SE$ with standard normal distribution, and the t-test above can be replaced by a z-test.

Example: According to the drinking water standard the maximal allowed lead content is $\mu_0=10\;\mu\,g/l$. Given $N=11$ samples taken from the tap water shown below, determine whether the lead content is significantly higher than the standard based on $\alpha=0.05$.

  $$11.70,\;9.39,\;11.78,\;10.66,\;11.07,\;8.93,\;9.63,\;12.08,\;12.93,\;10.62,\;11.50$$ (29)

The null hypothesis is $H_0:\;\mu=\mu_0=10$, i.e., there is no difference between the mean lead content level of the tap water and the standard. The sample mean and sample standard deviation can be found from the data samples as $\bar{x}=10.9353$ and $S=1.2318$, respectively, and the test statistic value $t^*=2.5182$ is outside the interval defined by the critical value $t_{\alpha/2}=t_{0.025}=-2.2281$, i.e., $t^*$ is in the critical region (red areas). Alternatively, we can find the p-value $p=0.0305$ (the blue areas), which is smaller than $\alpha=0.05$ (the red areas). Based on either of the two equivalent results, we conclude that the lead content is significantly higher than the standard.

We can also find the confidence interval of the mean $\mu$ based on $\bar{x}$ and $\alpha$ in terms of its upper and lower limits satisfying:

  $$P(L\le \mu \le U)=(1-\alpha)\;100\%$$ (30)

The null hypothesis is $H_0:\;\bar{x}=\mu$, i.e., the sample mean is the same as the mean of the distribution, and the test statistic is $t=(\bar{x}-\mu)/(S/\sqrt{N})=(\bar{x}-\mu)/\mbox{ESE}$.

If the sample size is large enough, e.g., $\nu=N-1>30$, the sample variance $S^2$ can be assumed to be approximately the same as the true variance $\sigma^2$, and the test statistic $t\sim {\cal T}_{\mu}(t)$ can be approximated by $z\sim {\cal N}(z,0,1)$. In this case, we can use the Z-test. Based on the z-Table we can find the critical values $z_{\alpha/2}$ and $z_{1-\alpha/2}=-z_{\alpha/2}$ satisfying the following:

  $$P(z_{\alpha/2} \le z \le z_{1-\alpha/2}) =\int_{z_{\alpha/2}}^{z_{1-\alpha/2}} {\cal N}(z,0,1)\;dz=1-\alpha,$$ (31)

i.e.,

$$P(-\infty<z<z_{\alpha/2})=\int_{-\infty}^{z_{\alpha/2}} {\cal N}(z,0,1)\;dz$$

$$= P(z_{1-\alpha/2}<z<\infty)=\int_{z_{1-\alpha/2}}^{\infty}{\cal N}(z,0,1)\;dz =\alpha/2$$

For example, if $\alpha=0.05$, $\alpha/2=0.025$, we can find $z_{\alpha/2}=z_{0.025}=1.96$.

We can further find the lower and upper limits of the confidence interval for $\mu$, based on the fact that the probabilities of the following equivalent events are the same:

$$P(z_{\alpha/2} \le z \le z_{1-\alpha/2}) =P\left(z_{\alpha/2} \le \frac{\bar{x}-\mu}{\sigma/\sqrt{N}} \le z_{1-\alpha/2}\right)$$

$$= P\left(\bar{x}-z_{\alpha/2}\frac{\sigma}{\sqrt{N}} \le \mu \le \bar{x}+z_{\alpha/2}\frac{\sigma}{\sqrt{N}}\right) =P(L\le \mu \le U)=1-\alpha$$

where

  $$L=\bar{x}+z_{\alpha/2}\frac{\sigma}{\sqrt{N}}=\bar{x}+z_{\alpha/2... ...\; U=\bar{x}-z_{\alpha/2}\frac{\sigma}{\sqrt{N}}=\bar{x}-z_{\alpha/2}\mbox{SE}$$ (32)

are the lower and upper limits of the confidence interval for $\mu$ corresponding to the given $\alpha$.

However, if the sample size $N$ is not large enough, the pdf of the test statistic $t$ is a t-distribution with $\nu=N-1$, and we find the critical values $t_{\alpha/2}$ and $t_{1-\alpha/2}=-t_{\alpha/2}$ satisfying the following

  $$P(t_{\alpha/2} \le t \le t_{1-\alpha/2}) =\int_{t_{\alpha/2}}^{t_{1-\alpha/2}} {\cal T}_\nu(\tau)\;d\tau=1-\alpha,$$ (33)

or equivalently

$$P(-\infty<t<t_{\alpha/2})=\int_{-\infty}^{t_{\alpha/2}} {\cal T}_\nu(\tau)\;d\tau$$

$$= P(t_{1-\alpha/2}<t<\infty)=\int_{t_{1-\alpha/2}}^{\infty}{\cal T}_\nu(t)\;d\tau =\alpha/2$$

For example, assuming $N=11$, $\nu=N-1=10$, and $\alpha=0.05$, we can find from the t-Table $t_{0.025}=-2.2281$ and $t_{0.975}=-t_{0.025}=2.2281$, which is greater than $z_{0.05/2}=1.96$ based on normal distribution, due to the longer tails of the t-distribution. When the sample size $N$ becomes larger, ${\cal T}_{\nu}(t)={\cal T}_{N-1}(t)$ approaches the standard normal distribution $N(z,0,1)$, and $t_{\alpha/2}$ approaches $z_{\alpha/2}$. For example, when $\nu=1000$, $t_{0.025}=1.962$ is very close to $z_{0.025}=1.96$.

We can further find the lower and upper limits of the confidence interval for $\mu$, due to the fact that the probabilities of the following equivalent events are the same:

  $$P(t_{\alpha/2}\le t\le t_{1-\alpha/2}) =P\left(t_{\alpha/2}\le \f... ...ght) =\int_{t_{\alpha/2}}^{t_{1-\alpha/2}} {\cal T}_\nu(\tau)\; d\tau=1-\alpha$$ (34)

Then we can get the limits for the confidence interval of the true mean $\mu$ as:

  $$L=\bar{x}+t_{\alpha/2}\frac{S}{\sqrt{N}}=\bar{x}+t_{\alpha/2} \mb... ...\;\; U=\bar{x}-t_{\alpha/2}\frac{S}{\sqrt{N}}=\bar{x}-t_{\alpha/2} \mbox{ESE},$$ (35)

so that $P(L\le \mu\le U)=1-\alpha$.

Example: Based on the same data set in the previous example, we can find the critical value as $t_{\alpha/2}=t_{0.025}=-2.2281$ and $\mbox{ESE}=S/\sqrt{N}=0.3718$, and the lower and upper limits of the confidence interval of the mean can be found as $\bar{x}\pm t_{\alpha/2}=10.935\pm 2.228\times 0.372$, i.e.,

  $$P(10.107 <\mu < 11.764)=(1-\alpha) 100\%=95\%$$ (36)

The Matlab function ttest can be used to carry out all t-test discussed above.