Next: One-Sample t-Test Up: StatisticTests Previous: Statistic Hypothesis Tests
The following probability density functions (pdf) are commonly used in statistical hypothesis tests:
 (1)
(1)
 has a normal distribution denoted by
has a normal distribution denoted by
 , then
, then
 , and
, and
 (2)
(2)
 and
and  .
.
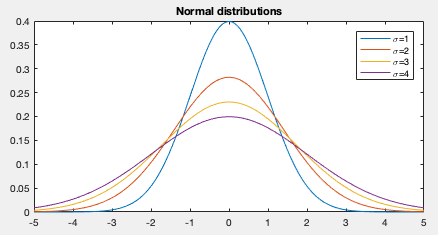
For example, if


 (3)
(3)
 -distribution:
-distribution:
 (4)
(4)
 is the degrees of freedom, and
is the degrees of freedom, and
 is the gamma function.
is the gamma function.
For example, if


 (5)
(5)
 have the normal distribution with
the same variance
have the normal distribution with
the same variance
 , i.e.,
, i.e.,
 , then
, then
 (6)
(6)
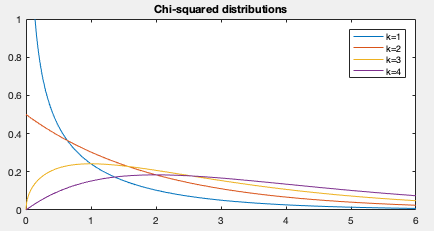
 (7)
(7)
 (8)
(8)
 and
and
 , then
, then
 (9)
(9)
 are i.i.d. samples of
are i.i.d. samples of
 , and
, and
 ,
then
,
then
 (10)
(10)
 degrees of freedom and
degrees of freedom and
 (11)
(11)
 degrees of freedom.
degrees of freedom.
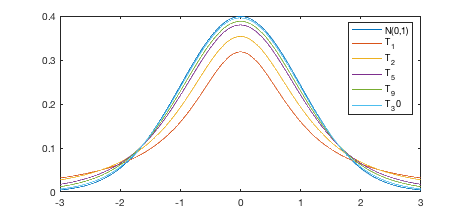
The t-distribution approaches the normal distribution when


 (12)
(12)
 are degrees of freedom, and
are degrees of freedom, and
 is
Beta function.
If
is
Beta function.
If  and
and  are independent and have Chi-squared
distribution:
are independent and have Chi-squared
distribution:
 (13)
(13)
 (14)
(14)
 (15)
(15)
 (16)
(16)
 (17)
(17)
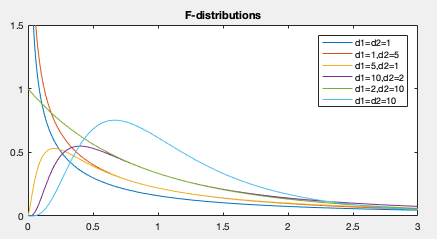
Assume






 (18)
(18)
 as
as  but a different variance
but a different variance  . The standard
deviation
. The standard
deviation
 , called the standard error and
denoted by SE, can be considered as the variability or noise.
Specially when
, called the standard error and
denoted by SE, can be considered as the variability or noise.
Specially when  , SE is the same as the standard deviation
, SE is the same as the standard deviation
 of the original distribution, but it decrease when
of the original distribution, but it decrease when  increases, and it approaches to zero when
increases, and it approaches to zero when  approaches to infinity.
approaches to infinity.
We can further define another random variable 




 (19)
(19)
 , called test statistic, we can carry out various
statistic tests called Z-test.
, called test statistic, we can carry out various
statistic tests called Z-test.
If the variance 
 (20)
(20)
 .
Now the random variable
.
Now the random variable  based on
based on  can be replaced by
another random variable
can be replaced by
another random variable  based on
based on  :
:
 (21)
(21)
 with a normal distribution,
with a normal distribution,  , as a test
statistic, has a t-distribution with
, as a test
statistic, has a t-distribution with  degrees of freedom.
degrees of freedom.
Given 