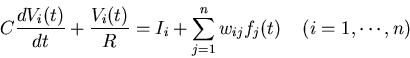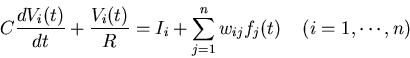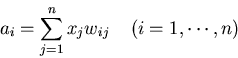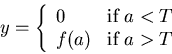Neural networks

In a neural network composed of a large number (say, n) of synaptically connected neurons, whether and how much a neuron is excited or inhibited depends on the synaptic stimulations it receives from other neurons. The intensity of each synaptic stimulation is in turn determined by (a) the level of excitation (or inhibition) of the neuron transmitting the signal, represented by its firing rate, and (b) the synaptic connectivity between the transmitting and receiving neurons, represented by the weight between the two neurons. And the over all evolution of the network, termed neurodynamics, can be described by the flowing equation for the ith neuron in the network:

$$C\frac{dV_i(t)}{dt}+\frac{V_i(t)}{R}=I_i+\sum_{j=1}^n w_{ij}f_j(t) \;\;\;\;(i=1,\cdots,n)$$

where weight w_ij represents the synaptic connectivity between the axon of the jth neuron (transmitting) and the dentrite of the ith neuron (receiving), f_j is the firing rate of the jth neuron related to its membrane potential V_j(t) by

f_j(t)=g(V_j(t))

and I_i is the external current injected into the ith neuron, representing the external stimulation. As mentioned before, if we treat g as dimensionless and f as voltage, then the weight w_ij has the dimension of a conductance (current/voltage), representing how easy it is for current to flow through the synapse from the jth neuron to the ith neuron. And the larger w_ij, the more the ith neuron is affected by the jth one.

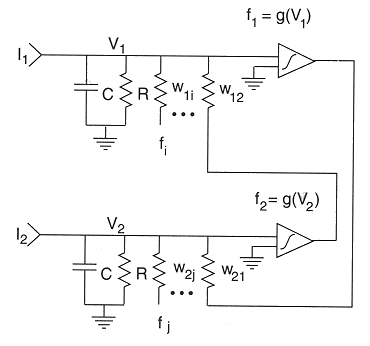
As solving such a large simultaneous differential equation system (of n equations) is in general very difficult, we further simplify the problem by ignoring the temporal behavior of the system and concentrating on the magnitudes of the output of a neuron as a function of the inputs from other neurons. The membrane potential of the ith neuron in this much simplified model becomes

$$a_i=\sum_{j=1}^n x_j w_{ij}\;\;\;\;(i=1,\cdots,n)$$

where a_i represents the activation of the receiving neuron, x_j represents the signal intensity transmitted by the jth neuron ( 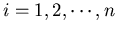$i=1, 2, \cdots, n$, assuming there are n of them), and w_ij represents the synaptic connectivity from the jth neuron to the ith neuron. If the activation level a is higher than the threshold, the neuron is excited to generate action potentials which will travel along its axon to other neurons down stream. The intensity of this output signal, represented by the firing rate, is a function of the activation

$$y=\left\{ \begin{array}{ll} 0 & \mbox{if $a<T$ } \\ f(a) & \mbox{if $a>T$ } \end{array} \right.$$

where T represents the threshold, y the output signal (firing rate) generated by the neuron, and f is a function such as the sigmoidal function as discussed above. This model is in the heart of many neural network algorithms. But note that all these algorithms ignore the temporal behaviors of the system.