


Next: Neural networks
Up: No Title
Previous: Adapting Model
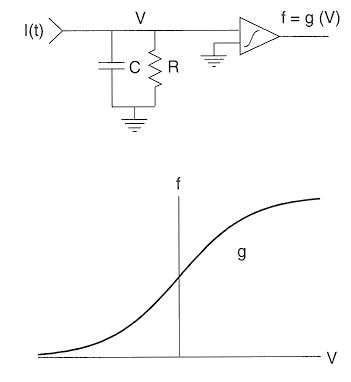
The firing rate model is used in most artificial neural networks. The dynamics
of this model is exactly the same as the integrate-and-fire model discussed
above. The only difference here is that the firing rate f is assumed to be
a continuous and nonlinear function of V(t)
f=g(V)
As function g relates membrane potential (voltage in Volt) to firing rate
(frequency in Hertz), it has the dimension of Hertz/Volt. But we could just
treat g as a dimensionless function for simplicity if we can accept to treat
f as if it is a voltage representing the signal intensity transmitted along
the axon (not to be confused with the intensity of the action potentials).
The most commonly used g is a sigmoidal function of V(t)
where c is some constant. The continuous firing rate model is obtained by
replacing the switch and the spike generator with a block simulating function
g, as shown in the figure.
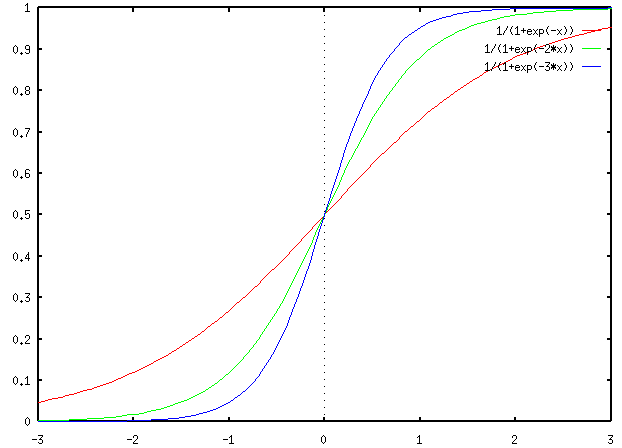
The sigmoidal function is used in many neural network models. Note that the
constant c determines the slope of the transition.
Several points need to be made regarding this firing rate model:
- The threshold for an action potential to be generated is not accounted
for. In fact, any small change in I(t) will affect V(t) and thereby
the firing rate f. When V(t) is small (around 0) the firing rate
f=g(V) is approximately a linear function of V(t).
- The non-zero firing rate g(0)=0.5 at V=0 represents the spontaneous
firing not related to any stimuli. And an excitatory stimulus will cause
a positive current I to increase V(t) (depolarization) and thereby a
higher firing rate, while an inhibitory stimulus will cause a negative
current to decrease V(t) (hyperpolarization) and thereby a lower
firing rate.
- g(V) is a saturating function which approaches 1 when
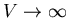 and 0 when
and 0 when
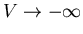 .
This is to model the fact that the firing rate of a neuron can never
exceed an upper limit no matter how much a neuron is excited, neither
can it be negative.
.
This is to model the fact that the firing rate of a neuron can never
exceed an upper limit no matter how much a neuron is excited, neither
can it be negative.



Next: Neural networks
Up: No Title
Previous: Adapting Model
Ruye Wang
1999-09-20

