Neuronal Model

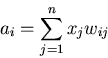
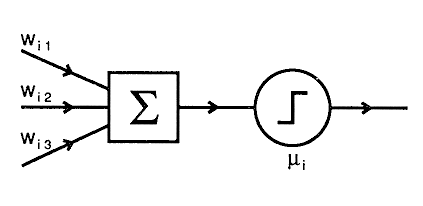
Whether and how much a neuron is excited or inhibited depends on the synaptic stimulations it receives from other neurons. The intensity of each synaptic stimulation is in turn determined by the level of excitation (or inhibition) of the neuron transmitting the signal and the synaptic connectivity between the transmitting and receiving neurons. This process can be modeled mathematically by

$$a_i=\sum_{j=1}^n x_j w_{ij}$$

where a_i represents the activation of the ith neuron in a population of n neurons, x_i represents the signal intensity transmitted by the jth neuron ( $j=1, 2, \cdots, n$), and w_ij represents the synaptic connectivity from the jth neuron to the ith neuron.

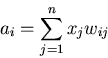
If the activation level a_i is higher than the threshold represented by $\mu_i$, the receiving neuron is excited to generate action potentials that travel along its axon to other neurons down stream. The intensity of this output signal is a function of the activation

$$y_i=\left\{ \begin{array}{ll} 0 & \mbox{if $a<\mu_i$ } \\ f(a_i) & \mbox{if $a>\mu_i$ } \end{array} \right.$$

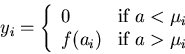
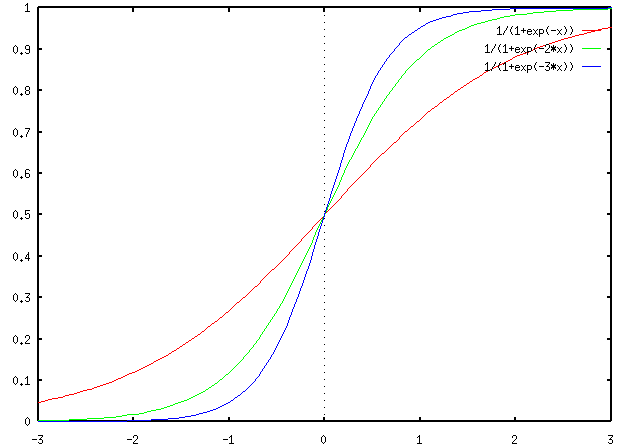
In some other mathematical models for a single neuron, an sigmoidal function is used as the function f(a):