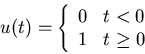Modeling RF of Retina Cells III - Time Domain

Next we model the RF in the time domain. The response r(t) of the midget ganglion cells to a step input defined as

$$u(t)=\left\{ \begin{array}{ll} 0 & t<0 \\ 1 & t\geq 0 \end{array} \right.$$

has both the transient and the maintained parts and can be modeled by

r(t)=T[ s(t) ]=h(t)=[k_m + k_t exp(-at)]u(t)

where k_m and k_t are, respectively, the magnitudes of the maintained and transient components, a is a parameter that determines how fast the transient response diminishes, and u(t) is a unit step function.

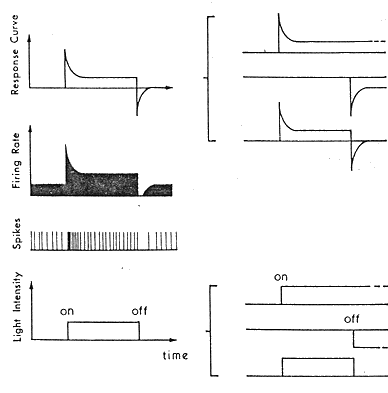
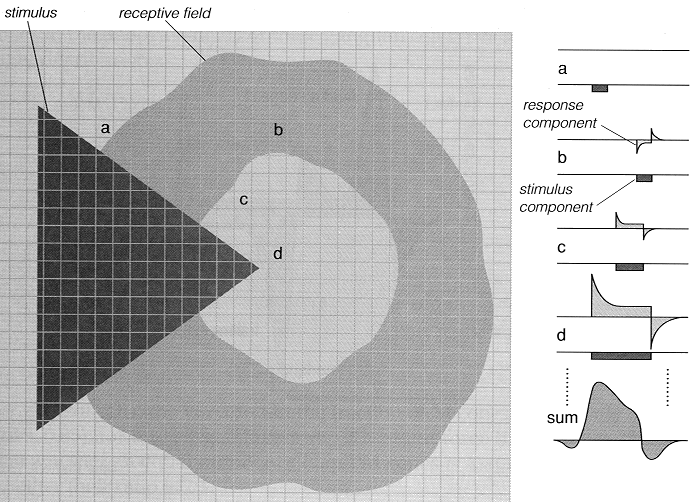
A simmple impulse stimulus, a light with constant intensity (e.g., 1 for simplicity) which is turned on at time moment t=t₁ and off at t-t₂can be represented by two step functions:

s(t)=u(t-t₁)-u(t-t₂)

Approximating the RF as a linear system and apply superposition, the response to this stimulus is

r(t)=T[ s(t) ]=T[ u(t-t₁)]-T[u(t-t₂)]

as shown in this figure:

Combining both the spatail and temporal aspects, the RF can be modeled by its response to a unit step input over the entire RF:

$$f(x,y,t)\stackrel{\triangle}{=}f(x,y)h(t)$$

Note that here h(t) is the temporal response to a step function u(t), instead of the usual impulse function 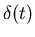$\delta(t)$. Since this spatiotemporal response function is a product of spatial response f(x,y) and temporal response r(t), we see that the spatial and temporal aspects of the RF can be separated. However, this separability no longer hold in some cortical cells as we will when we discuss modeling motion sensitive cells in the visual cortex.

Given the spatiotemporal desription f(x,y,t) of the RF of a ganglion cell, its temporal response to a certain stimulus s(x,y,t) can be computed and then compared to the experimental result:

$$r(t)=\int \int f(x,y,t) s(x,y,t) dx \mbox{ }dy \mbox{ }dt$$

An example is shown in this figure: