The optics of the eye

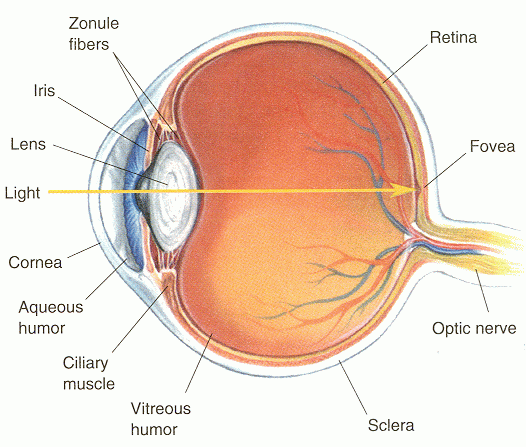
The basic optic function of the eye is to form an image of whatever object being looked at (fixated on) on the retina. This image formation is done by the combination of the cornea and the lens which behaves like a convex lens. The focus length of this lens is adjustable by the muscles attached to it according to the distance of the object so that its image is always formed on the retina in normal situation.

The simple relationship between the focal length f of the lens and the distances of the object and its image is

$$\frac{1}{d_o}+\frac{1}{d_i}=\frac{1}{f}$$

where d_o and d_i are the distances from the lens to the object and its image, respectively. For a given f, distant object (large d_o)

In the human eye, as the image always needs to be formed on the retina, d_i is fixed to be the distance between the lens and the retina, which is about 0.017 meters (17 mm), and the focal length of the lens need to be adjuected as a function of the distance of the object:

$$f=\frac{0.017 d_o }{d_o+0.017}$$

If, for various reasons, the eye fails to focus the images on the retina (either in front or behind the retina), eye glasses are needed to change the focal length so that the image can still be formed on the retina.

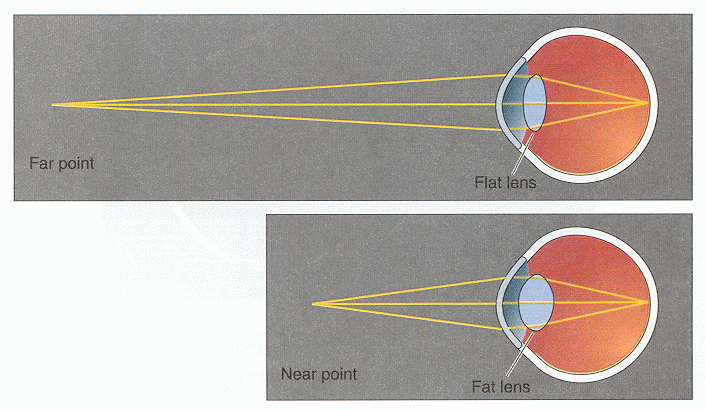
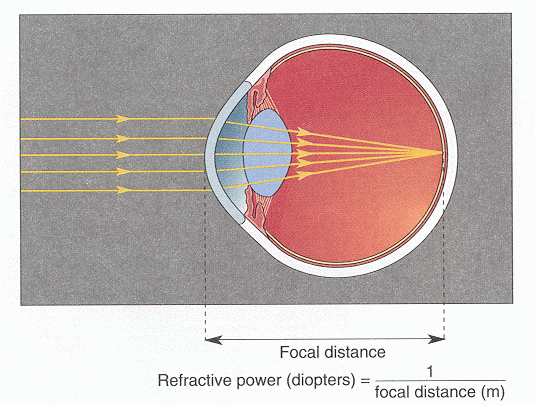
The power of a lens to bend the incoming light is measured by diopter, defined as the reciprocal of the focal length in meter. To see objects of different distances, the power of the lens needs to be changed accordingly. When the object is far away ( $d_o \rightarrow \infty$), its image is formed at the distance equal to the focal length ( d_i=f=0.017 mm); however, when the object is close, its image will be formed farther away from the lens (d_i>f). 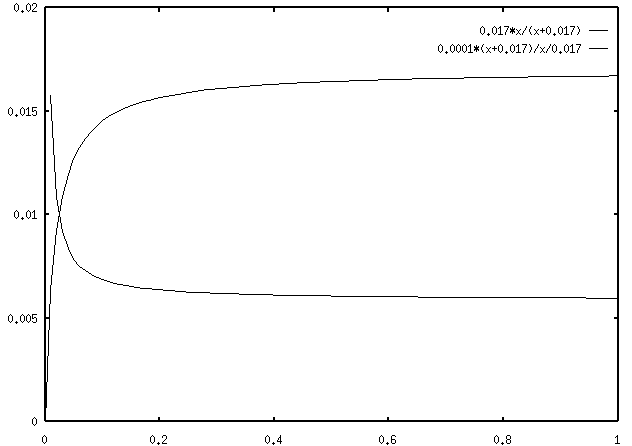For the image to still be formed on the retina, the lens needs to change its shape to increase its power (shorten f). As one can see in the plot below (showing f and 1/f as functions of object distance d_o, given d_i=17 mm), major adjustment of the lens is needed only when viewing objects within the range of about half a meter. For example, the focal length needs to be at 0.0145 meters for an object at 0.4 meters, or 0.0163 meters for an object at 0.4 meters. To view any object farther away than 0.5 meters, the lens needs to be pretty relaxed so that f is very close to 0.017 meters.

 

Figure: Focal length and power of eye as functions of object distance