From the fact that the trichromatic system can distinguish more colors than the dichromatic system, which in turn can distinguish more colors than the monochromatic system, it seems obvious that the more different types of photoreceptors the vision system has, the more values are available to represent a color, and the more comparisons can be made to distinguish more colors. As trichromatic system still cannot tell all possible colors apart, how many different types of receptors are necessary to do so?
The key here is to be able to uniquely represent in the visual system the
energy spectral distribution ![]() of an incoming light, which determines
the physical property of the light (but not necessarily its perceived color). To
approach the problem, we discretize the continuous spectral distribution
of an incoming light, which determines
the physical property of the light (but not necessarily its perceived color). To
approach the problem, we discretize the continuous spectral distribution ![]() by approximating it by
by approximating it by ![]() values
values
![]() , each
representing the energy contained in one of
, each
representing the energy contained in one of ![]() segments of the distribution. Now
the response of the
segments of the distribution. Now
the response of the ![]() receptor to the light becomes
receptor to the light becomes
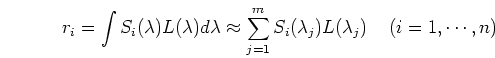
The number ![]() of discrete values
of discrete values ![]() depends on the details of the
spectral distribution of the incoming lights, and usually
depends on the details of the
spectral distribution of the incoming lights, and usually ![]() needs to be much
greater than
needs to be much
greater than ![]() to describe the various distributions of the incoming lights.
This is why
to describe the various distributions of the incoming lights.
This is why ![]() types of receptors are not enough to tell all colors apart.
types of receptors are not enough to tell all colors apart.