Example: Sampling Sinusoidal Signals

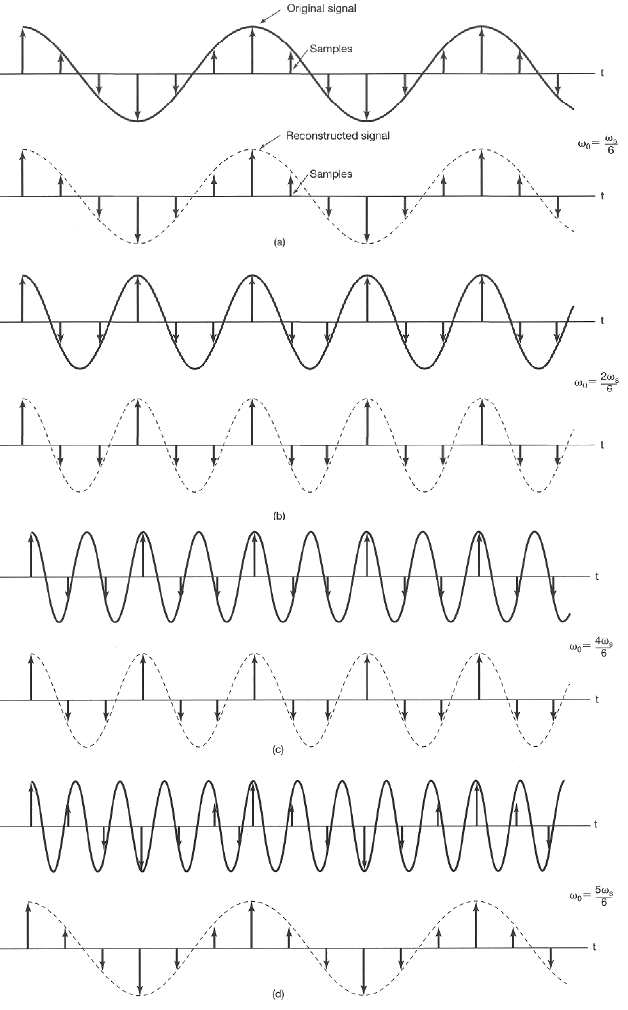
To demonstrate the sampling theorem, the figure below shows the sampling of sinusoidal signals of various frequencies. As can be seen, when the frequency is higher than half of the sampling rate, aliasing occurs.

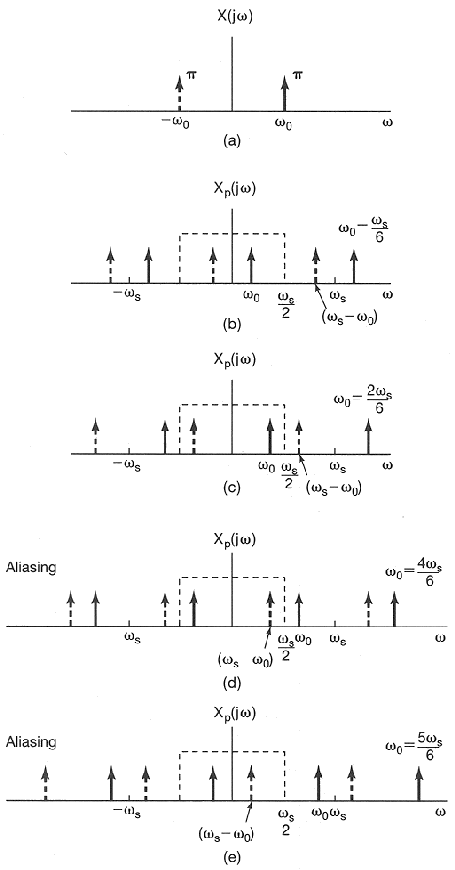
The same sampling process can be further illustrated in the frequency domain as shown in the figure below. The spectrum of the sinusoidal signal $x(t)=cos(\omega_0 t)=cos(2\pi f_0)$ is $X(\omega)=\delta(\omega-\omega_0)+\delta(\omega+\omega_0)$, containing two delta impulses at $\omega=\omega_0$ on either side of the origin, as shown in (a).

To sample the signal, x(t) is multiplied by a comb p(t) in time domain, or equivalently, its spectrum $X(\omega)$ is convolved with $P(\omega)$ to become $X_p(\omega)=X(\omega) * P(\omega)$, as shown in (b). Note that the period of $P(\omage)$ equals to the sampling frequency $\omega_s=1/T_s$, and the convolution has infinite copies of $X(\omega)$ (the two delta impulses) separated by distance $\omega_s$.

In (b) and (c), $\omega_0<\omega_s/2$, i.e., the original copy of $X(\omega)$ is inside the window of the ideal lowpass filter (with cut-off frequency $\omega_s/2$) which can perfectly reconstruct the original signal x(t) from its samples.

In (d) and (e), $\omega_0>\omega_s/2$, i.e., the original copy of $X(\omega)$is outside the window of the ideal lowpass filter. Instead, the lowpass filter will catch the copies of $X(\omega)$ in the next higher frequency range (both positive and negative). In the case, the reconstructed signal by lowpass filtering will appear to be at frequency $\omega_s-\omega_0$ (represented by the impulses inside the window of the ideal filter), which is lower than the actual frequency $\omega_0$, i.e., aliasing occurs.

The sampling of a sinusoidal function is illustrated in this web demo