The comb function and its spectrum

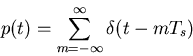
The comb (or sampling) function is a sequency of infinite delta impulses uniformly distributed in time (or space):

$$p(t)=\sum_{m=-\infty}^{\infty} \delta(t-m T_s)$$

where T_s is the interval between two neighboring impulses, and f_s = 1/T_s is the sampling rate.

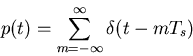
As p(t) is periodic (period T_s), it can be Fourier expanded:

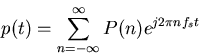
$$p(t)=\sum_{n=-\infty}^{\infty} P(n)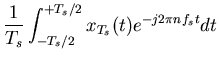e^{j2\pi nf_s t}$$

where the expansion coefficients are

$$\frac{1}{T_s} \int_{-T_s/2}^{+T_s/2} x_{T_s}(t) e^{-j2\pi nf_s t} dt$$ P(n) =

$$\frac{1}{T_s} \int_{-T_s/2}^{+T_s/2} [\sum_{m=-\infty}^{\infty} \delta(t-m T_s) ] e^{-j2\pi nf_s t} dt$$ =

$$\frac{1}{T_s} \int_{-T_s/2}^{+T_s/2} \delta(t) e^{-j2\pi nf_s t} dt = \frac{1}{T_s} e^{0} =\frac{1}{T_s}\;\;\;\;\;\;(n=0, \pm 1, \pm 2, \cdots)$$ =

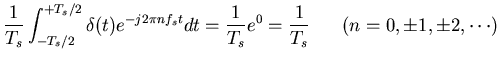Now the expression for p(t) can be written as:

$$p(t)=\sum_{m=-\infty}^{\infty} \delta(t-m T_s) = \sum_{n=-\i... ... t} =\frac{1}{T_s} \sum_{n=-\infty}^{\infty} e^{j2\pi nf_s t}$$

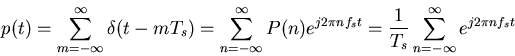
Again, the coefficients can be considered as the discrete, non-periodic spectrum of the comb function:

$$P(f)=\sum_{n=-\infty}^{\infty} P(n)\delta(f-nf_s) = \frac{1}{T_s}\sum_{n=-\infty}^{\infty} \delta(f-nf_s)$$

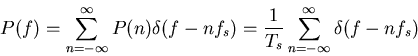
Note that the interval between two neighboring impulses is the sampling rate f_s=1/T_s. That is, high sampling rate (small interval between two neighboring sampling impulses) of p(t) corresponds to large gap T_s in it spectrum.