


Next: KLT Completely Decorrelates the
Up: pca
Previous: Covariance and Correlation
The Principal Component Transform is also called Karhunen-Loeve
Transform (KLT), Hotelling Transform, or Eigenvector Transform.
Let 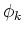 and
and 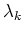 be the kth eigenvector and eigenvalue of the
covariance matrix
be the kth eigenvector and eigenvalue of the
covariance matrix 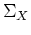 :
:
or in matrix form:
We can construct an 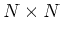 matrix
matrix 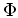
Since the columns of 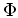 are the eigenvectors of a symmetric (Hermitian if
are the eigenvectors of a symmetric (Hermitian if
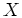 is complex) matrix
is complex) matrix 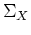 ,
, 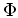 is orthogonal (unitary):
is orthogonal (unitary):
and we have
or in matrix form:
where
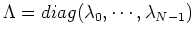 . Or, we have
. Or, we have
We can now define the orthogonal (unitary if 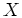 is complex) Principal
Component Transform of
is complex) Principal
Component Transform of 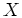 . The forward transform:
. The forward transform:
and the inverse transform
The ith component of the forward transform 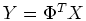 is the projection of
is the projection of
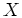 on
on 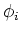 :
:
and the inverse transform 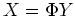 represents
represents 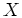 in the N-dimensional space
spanned by
in the N-dimensional space
spanned by 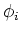
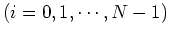 :
:



Next: KLT Completely Decorrelates the
Up: pca
Previous: Covariance and Correlation
Ruye Wang
2004-09-29
![]() and
and ![]() be the kth eigenvector and eigenvalue of the
covariance matrix
be the kth eigenvector and eigenvalue of the
covariance matrix ![]() :
:
![\begin{displaymath}\left[ \begin{array}{ccc}\cdots &\cdots &\cdots \\
\cdots &...
...a_k\left[ \begin{array}{c} \ \phi_k \ \ \end{array} \right] \end{displaymath}](img47.png)
![\begin{displaymath}\left[ \begin{array}{ccc}\cdots &\cdots &\cdots \\
\cdots &...
... &\cdots \ \cdots &\cdots &\lambda_{N-1} \end{array} \right]
\end{displaymath}](img53.png)
![]() is complex) Principal
Component Transform of
is complex) Principal
Component Transform of ![]() . The forward transform:
. The forward transform:
![\begin{displaymath}Y=\left[ \begin{array}{l} y_0 y_1 \cdots y_{N-1} \end...
...T_0 \phi^T_1 \cdots \phi^T_{N-1} \end{array} \right] X \end{displaymath}](img56.png)
![\begin{displaymath}X=\Phi Y=[ \phi_0, \phi_1, \cdots, \phi_{N-1} ]
\left[ \begin{array}{l} y_0 y_1 \cdots y_{N-1} \end{array} \right]
\end{displaymath}](img57.png)
