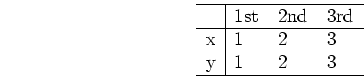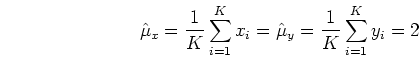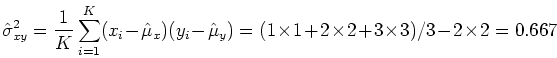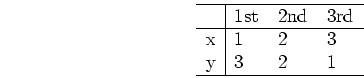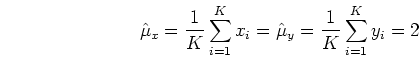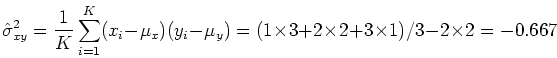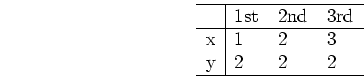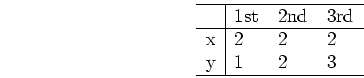Next: The Principal Component Transform
Up: pca
Previous: Multivariate Random Signals
The mean and the variance of two variables 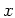 and
and 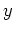 can be estimated by
averaging the outcomes of the random experiment concerning the variables repeated
can be estimated by
averaging the outcomes of the random experiment concerning the variables repeated
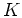 times:
times:
and their covariance can be estimated as
Examples
Consider the following examples showing the covariance 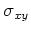 between
two random variables
between
two random variables 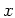 and
and 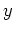 under various situations.
under various situations.
- Example 1: assume the experiment concerning
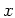 and
and 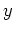 is repeated
is repeated 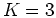 times with the outcomes:
times with the outcomes:
The means and covariance of 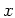 and
and 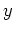 can be estimated as
can be estimated as
We see that in this case 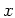 and
and 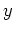 are highly (maximally) correlated.
are highly (maximally) correlated.
- Example 2: assume the outcomes of the 3 experiments are
Similarly, we get
indicating that the two variables are highly negatively correlated.
- Example 3: assume the outcomes are:
We have
indicating that the two variables are totally uncorrelated (unrelated).
- Example 4: assume the outcomes are:
We have
indicating that the two variables are totally uncorrelated (unrelated).
- Example 5: assume the experiment is carried out
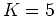 times (combination
of examples 4 and 5) with the outcomes:
times (combination
of examples 4 and 5) with the outcomes:
We still have
indicating that the two variables are totally uncorrelated (unrelated).



Next: The Principal Component Transform
Up: pca
Previous: Multivariate Random Signals
Ruye Wang
2004-09-29
![]() and
and ![]() can be estimated by
averaging the outcomes of the random experiment concerning the variables repeated
can be estimated by
averaging the outcomes of the random experiment concerning the variables repeated
![]() times:
times:
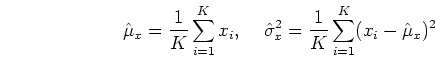
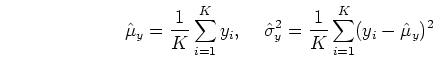
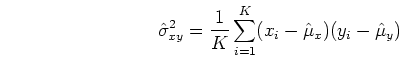
![]() between
two random variables
between
two random variables ![]() and
and ![]() under various situations.
under various situations.