A Thinning Algorithm

Purpose: Convert binary shapes obtained from edge/boundary detection or thresholding to 1-pixel wide lines. For example, the thresholded version of hand written or printed alphanumerics can be thinned for better represetation and further processing.

Method: iteratively delete pixels inside the shape to shrink it without shortening it or breaking it apart.

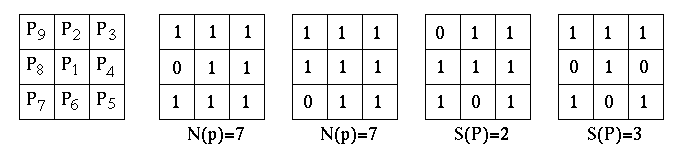
Some Definitions: To decide whether an edge pixel $P_1$ should be deleted, consider its 8 neighbors in the 3 by 3 neighborhood, $P_2$, $P_3$, $P_4$, $P_5$, $P_6$, $P_7$, $P_8$ and $P_9$, and define:

• $N(P_1)$: number of non-zero neighbors:
  
  $$N(P_1)=P_2+P_3+\cdots+P_9$$
  
  

• $S(P_1)$: number of 0 to 1 (or 1 to 0) transitions in the sequence $(P_2,P_3,\cdots, P_9)$.

The Algorithm: This is a 2-pass process:

• Pass 1: Mark any edge pixel $P_1=1$ not satisfying at least one of the following conditions (to be deleted in second step):
  • $N(P_1)=0$ (an isolated point)
  • $N(P_1)=1$ (tip of a line)
  • $N(P_1)=7$ (located in concavity)
  • $N(P_1)=8$ (not a boundary point)
  • $S(P_1)\ge 2$ (on a bridge connecting two or more edge pieces)
• Pass 2: Deleted all marked edge points.

A problem: When part of the shape is only 2-pixel wide, all pixels are boundary points and will be marked and then deleted. We want to delete only one side at a time.

The Solution: A two-step process:

• Step 1: Delete all deletable point in the S, E, NW and NE boundaries.
• Step 2: Delete all deletable point in the N, W, SE and SW boundaries.

Modified Algorithm: Repeat until no more change can be made:

• 1: Mark all pixels satisfying ALL of the following: $(P_1=1)$ and $(2\le N(P_1) \le 6)$ and $(S(P_1)=1)$ and $(P_2\cdot P_4\cdot P_6=0)$ and $(P_4\cdot P_6\cdot P_8=0)$ and $(P_7\ne 0)$.
• 2: Delete all marked pixels.

• 3: Mark all pixels satisfying the following:
  
  $$[P_1=1]\;\wedge\;[2\le N(P_1)\le 6]\;\wedge\;[S(P_1)=1]\;\wed... ... P_8=0]\;\wedge\;[P_2\cdot P_6\cdot P_8=0]\;\wedge\;[P_7\ne 0]$$
  
  

• 4: Delete all marked pixels.

Let $A_i$ represent the event ``$P_i=0$''. Then $[P_2\cdot P_4\cdot P_6=0]\;\wedge\;[P_4\cdot P_6\cdot P_8=0]$ above can be represented by:

$$(A_2\vee(A_4\vee A_6))\wedge((A_4\vee A_6)\vee A_8) =A_4\vee A_6\vee(A_2\wedge A_8)$$

i.e.,

$$(P_4=0) \vee (P_6=0) \vee (P_2=P_8=0)$$

This is either an E edge ($P_4=0$), an S edge ($P_6=0$), an NW edge ($P_2=P_8=0$), an NE edge ($P_4=P_2=0$), or an SW edge ($P_6=P_8=0$). However, the additional condition $P_7\ne 0$ excludes an SW edge.

Similarly, we see hat edges on N, W, SW, or SE side will be deleted in the second pass.