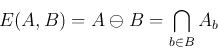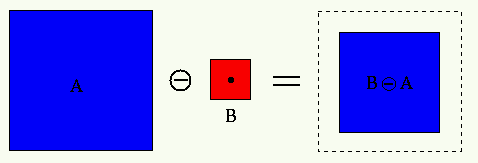Next: A Thinning Algorithm
Up: morphology
Previous: morphology
Language of set theory
Let 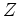 denote the set of all integers, and
denote the set of all integers, and 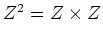 denote the
set of integer pairs
denote the
set of integer pairs 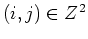 . The coordinates of a pixel
. The coordinates of a pixel
![$v[i][j]$](img4.png) in an image can therefore be considered as a component of
in an image can therefore be considered as a component of 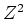 .
.
Let  and
and 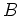 be two white regions in a black and white binary image.
Then they can be considered as two sets in
be two white regions in a black and white binary image.
Then they can be considered as two sets in 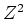 space, and their
components
space, and their
components
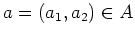 and
and
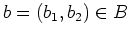 are just a pixel
inside each of the regions.
are just a pixel
inside each of the regions.
In a binary image, an object of a certain shape can be represented by a
set of either 4- or 8-connected white pixels in white background. To carry
out certain operations on the shape of the object, the object and its back
ground are mathematically represented as sets.
In general, a set is defined as a group of components all having certain
properties or satisfying certain conditions:
- Object:
- Background:
where 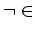 means ``not belong to''.
means ``not belong to''.
Basic definitions:
- Translation: The translation of
 by
by 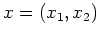 is
is
where
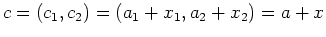 .
.
- Reflection: The reflection of
 is
is
Here the reflection is with respect to a specific origin, such as a point
center in the shape, e.g., the center of the shape.
- Complement: The complement of
 is
is
- Difference: The difference between
 and
and 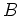 is
is
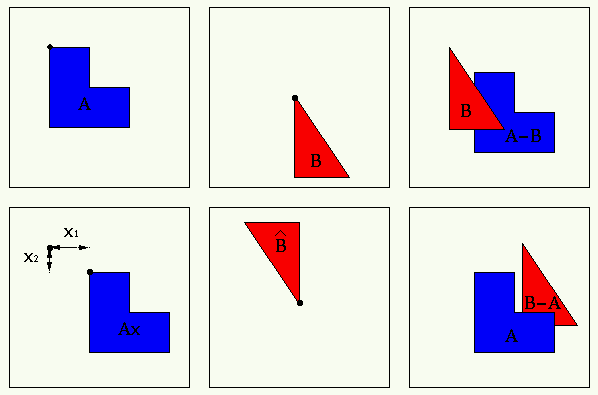
Below, a structuring element 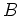 is a binary object used in varioius
morphology operators. All elements
is a binary object used in varioius
morphology operators. All elements 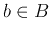 are measured with respect to the
origin
are measured with respect to the
origin 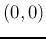 located at the center of the object. For example, if
located at the center of the object. For example, if 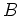 is a
is a
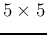 square, then for any
square, then for any
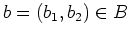 ,
,
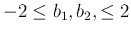 .
.
Dilation
where 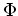 represents empty set. Alternatively,
represents empty set. Alternatively,
- Find reflection
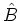 of set
of set 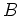 by flipping it about its origin.
If
by flipping it about its origin.
If 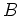 is central symmetric, this step makes no difference;
is central symmetric, this step makes no difference;
- Translate (shift, slide)
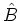 by displacement
by displacement 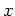 over
over  ;
;
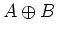 is the set of all displacements
is the set of all displacements 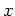 's that keep the
intersect (overlap) of
's that keep the
intersect (overlap) of 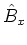 and
and  non-empty (keep them
``in touch'').
non-empty (keep them
``in touch'').
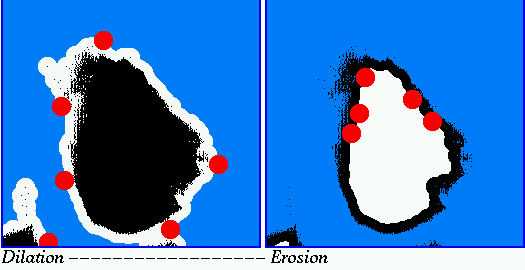
- Dilation of a binary image shape
 by
by 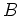 expands the shape by
half of the size of
expands the shape by
half of the size of 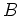 .
.
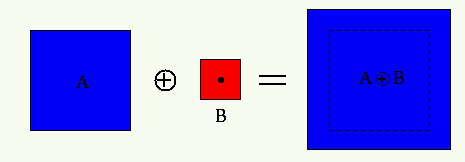
As typically the structuring element  is symmetric (either central
symmetric or symmetric with respect to its vertical or horizontal axis),
the reflection part of the dilation definition will be dropped in the
following.
is symmetric (either central
symmetric or symmetric with respect to its vertical or horizontal axis),
the reflection part of the dilation definition will be dropped in the
following.
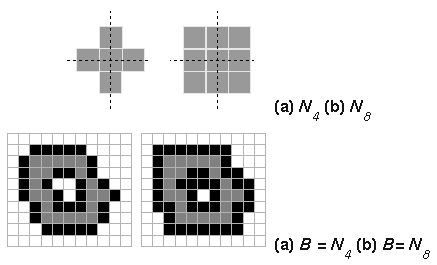
For these simplest structuring elements, dilation can be carried out
by setting all background pixels (with value "0") 4- or 8-connected to
each object pixel (with value "1") to the value "1".
Erosion
Alternatively,
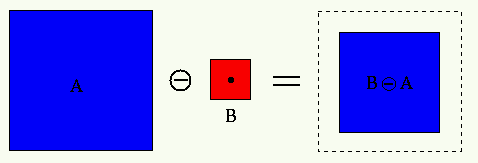
If the same simple structuring elements are used, erosion can be carried
out by setting each object pixel (with value "1") 4- or 8-connected to a
background pixel (with value "0") to the value "0".
Properties of dilation and erosion
- Commutative:
- Non-commutative:
- Associative:
-
-
-
- The complement of the erosion of
 by
by 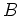 is the same as the
dilation of complement of
is the same as the
dilation of complement of  by
by 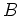 :
:
- The complement of the dilation of
 by
by 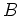 is the same as the
erosion of complement of
is the same as the
erosion of complement of  by
by 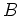 .
.
Proof:
Since set 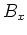 is contained in
is contained in  , i.e.,
, i.e.,
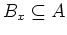 , it has
no overlap with the complement of
, it has
no overlap with the complement of  , i.e.,
, i.e.,
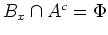 ,
and the above equation can be written as:
,
and the above equation can be written as:
But the complement of this set of all 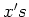 satisfying the condition
satisfying the condition
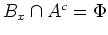 is the set of all
is the set of all 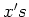 not satisfying the
condition, i.e.,
not satisfying the
condition, i.e.,
Taking complement on both sides above, and replacing  by
by 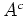 , we
get the second relation.
, we
get the second relation.
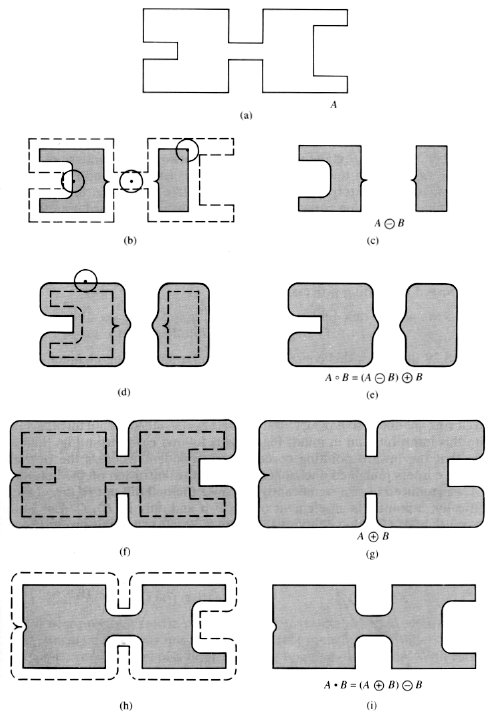
Opening
The opening of  and
and 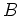 is the dilation of the erosion of
is the dilation of the erosion of  by
by 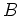 .
.
- Dilation and erosion are not a pair of opposite operations in
the sense that their effects do not cancel each other.
- The erosion carried out first eliminates small shapes (assumed to
be noise) as well as shrinking the object shape, while the following
dilation grows the object back (but not the noise).
Closing
The closing of  and
and 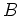 is the erosion of the dilation of
is the erosion of the dilation of  by
by 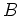 .
.
- The effect of dilation and erosion do not cancel each other.
- The dilation carried out first eliminates small holes inside the
object shape (assumed to be noise) as well as expanding the object
shape, while the following erosion shrinks the object back (but not
the noise).
Grayscale dilation and erosion
Morphological operations can be generalized to grayscale images. Here
neither the image nor the structuring element is binary any more, and the
Boolean operations (AND and OR, union and intersect) used for binary images
are replaced by addition, subtraction, maximum and minimum operations.
- Dilation:
where the maximum value is taken in the neighborhood of pixel ![$[m,n]$](img53.png) defined
by the structuring element
defined
by the structuring element 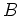 . Dilation tends to grow the white regions of
an image. If the structuring element has positive values, the resulting image
tends to be brighter.
. Dilation tends to grow the white regions of
an image. If the structuring element has positive values, the resulting image
tends to be brighter.
- Erosion:
where the minimum value is taken in the neighborhood of pixel ![$[m,n]$](img53.png) defined
by the structuring element
defined
by the structuring element 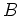 . Erosion tends to shrink the white regions of
an image. If the structuring element has positive values, the resulting image
tends to be darker.
. Erosion tends to shrink the white regions of
an image. If the structuring element has positive values, the resulting image
tends to be darker.
Applications:
- Extracting boundaries : The boundary of
 , denoted by
, denoted by 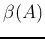 , can be
obtained as the difference of
, can be
obtained as the difference of  and its erosion
and its erosion 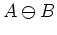 or dilation
or dilation
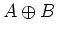 :
:
- Filling holes:
- Thinning:
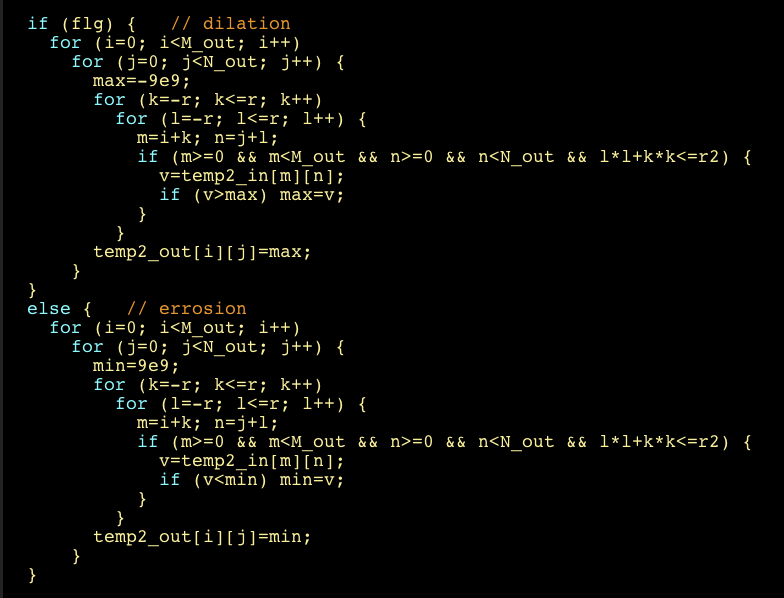
Example:

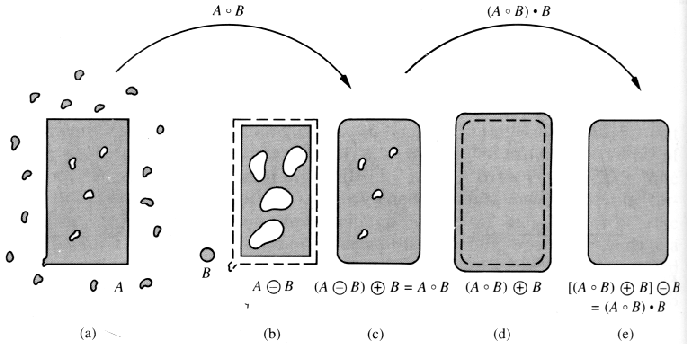

Example:
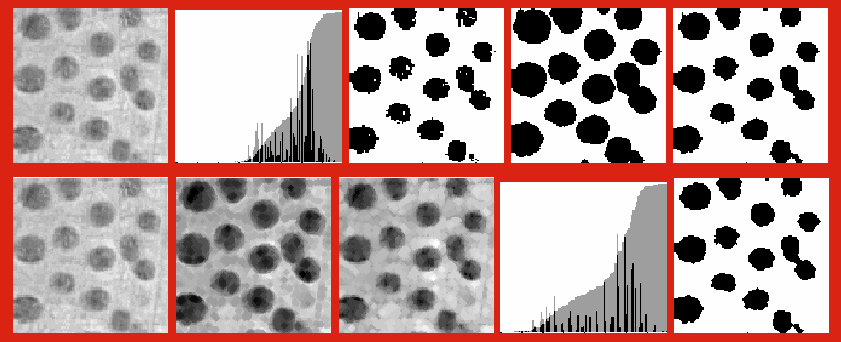
Binary morpohology (top): original image, histogram, binary image (threshold 160), erosion, dilation;
Gray-scale morphology (bottom): original image, erosion, dilation, histogram, binary image (threshold 130).



Next: A Thinning Algorithm
Up: morphology
Previous: morphology
Ruye Wang
2011-11-09
![]() denote the set of all integers, and
denote the set of all integers, and ![]() denote the
set of integer pairs
denote the
set of integer pairs ![]() . The coordinates of a pixel
. The coordinates of a pixel
![]() in an image can therefore be considered as a component of
in an image can therefore be considered as a component of ![]() .
.
![]() and
and ![]() be two white regions in a black and white binary image.
Then they can be considered as two sets in
be two white regions in a black and white binary image.
Then they can be considered as two sets in ![]() space, and their
components
space, and their
components
![]() and
and
![]() are just a pixel
inside each of the regions.
are just a pixel
inside each of the regions.

![]() is a binary object used in varioius
morphology operators. All elements
is a binary object used in varioius
morphology operators. All elements ![]() are measured with respect to the
origin
are measured with respect to the
origin ![]() located at the center of the object. For example, if
located at the center of the object. For example, if ![]() is a
is a
![]() square, then for any
square, then for any
![]() ,
,
![]() .
.
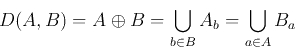

![]() is symmetric (either central
symmetric or symmetric with respect to its vertical or horizontal axis),
the reflection part of the dilation definition will be dropped in the
following.
is symmetric (either central
symmetric or symmetric with respect to its vertical or horizontal axis),
the reflection part of the dilation definition will be dropped in the
following.