Measures of Non-Gaussianity

The ICA method depends on certain measurement of the non-Gaussianity:

• Kurtosis

  Kurtosis is defined as the normalized form of the fourth central moment of a distribution:
  

  $$kurt(x)=E\{x^4\}-3(E\{x^2\})^2$$
  
  
  If we assume $x$ to have zero mean $\mu_x=E\{x\}=0$ and unit variance $\sigma^2_x=E\{x^2\}-\mu_x^2=1$, then $E\{x^2\}=1$ and $kurt(x)=E\{x^4\}-3$. Kurtosis measures the degree of peakedness (spikiness) of a distribution and it is zero only for Gaussian distribution. Any other distribution's kurtosis is either positive if it is supergaussian (spikier than Gaussian) or negative if it is subgaussian (flatter than Gaussian). Therefore the absolute value of the kurtosis or kurtosis squared can be used to measure the non-Gaussianity of a distribution. However, kurtosis is very sensitive to outliers, and it is not a robust measurement of non-Gaussianity.

  

• Differential Entropy - Negentropy

  The entropy of a random variable $y$ with density function $p(y)$ is defined as
  

  $$H(y)=-\int_{-\infty}^\infty p(y) log\; p(y) dy =-E\{ log \; p_i(y) \}$$
  
  
  An important property of Gaussian distribution is that it has the maximum entropy among all distributions over the entire real axis $(-\infty,\infty)$. (And uniform distribution has the maximum entropy among all distributions over a finite range.) Based on this property, the differential entropy, also called negentropy, is defined as
  
  $$J(y)=H(y_G)-H(y) \ge 0$$
  
  
  where $y_G$ is a Gaussian variable with the same variance as $y$. As $J(y)$ is always greater than zero unless $y$ is Gaussian, it is a good measurement of non-Gaussianity.

  This result can be generalized from random variables to random vectors, such as ${\mathbf y}=[y_1,\cdots,y_m]^T$, and we want to find a matrix ${\mathbf W}$ so that ${\mathbf y=Wx}$ has the maximum negentropy $J({\mathbf y})=H({\mathbf y_G)}-H({\mathbf y})$, i.e., ${\mathbf y}$ is most non-Gaussian. However, exact $J({\mathbf y})$ is difficult to get as its calculation requires the specific density distribution function $p({\mathbf y})$.

• Approximations of Negentropy

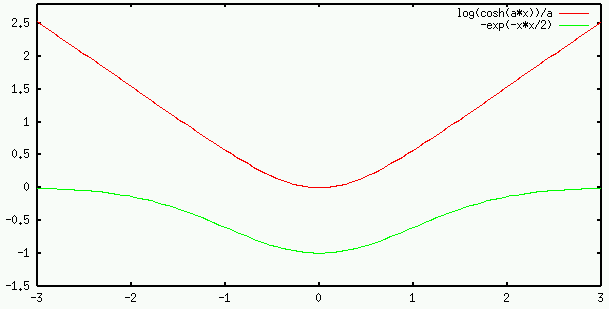
  The negentropy can be approximated by
  

  $$J(y)\approx \frac{1}{12}E\{y^3\}^2+\frac{1}{48} kurt(y)^2$$
  
  
  However, this approximation also suffers from the non-robustness due to the kurtosis function. A better approximation is
  
  $$J(y)\approx \sum_{i=1}^p k_i [ E\{G_i(y)\}-E\{G_i(g)\}]^2$$
  
  
  where $k_i$ are some positive constants, $y$ is assumed to have zero mean and unit variance, and $g$ is a Gaussian variable also with zero mean and unit variance. $G_i$ are some non-quadratic functions such as
  
  $$G_1(y)=\frac{1}{a} log\;cosh\;(a \;y),\;\;\;\;\;G_2(y) =-exp(-y^2/2)$$
  
  
  where $1 \le a \le 2$ is some suitable constant. Although this approximation may not be accurate, it is always greater than zero except when $x$ is Gaussian. In particular, when $p=1$, we have
  
  $$J(y)=[E\{ G(y)\}-E\{G(g)\}]^2$$
  
  
  Since the second term is a constant, we want to maximize $E\{ G(y) \}$ to maximize $J(y)$.