Generally speaking, a kernel is a continuous function ![]() that takes
two arguments
that takes
two arguments ![]() and
and ![]() (real numbers, functions, vectors, etc.) and maps
them to a real value independent of the order of the arguments, i.e.,
(real numbers, functions, vectors, etc.) and maps
them to a real value independent of the order of the arguments, i.e.,
![]() .
.
Examples:
Mercer's theorem:
A kernel is a continuous function that takes two variables ![]() and
and ![]() and map them to a real value such that
and map them to a real value such that ![]() .
.
A kernel is non-negative definite iff:
In association with a kernel ![]() , we can define an integral operator
, we can define an integral operator ![]() ,
which, when applied to a function
,
which, when applied to a function ![]() , generates another function:
, generates another function:
The eigenvalues and their correponding eigenfunctions of this operation
are defined as:
The eigenfunctions corresponding to the non-zero eigenvalues form a set
of basis functions so that the kernel can be decomposed in terms of them:
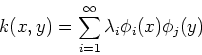
The above discussion can be related to a non-negative ![]() matrix
matrix
![\begin{displaymath}{\bf A}=\left[ \begin{array}{ccc} ...&...&...\\ ...&a[m,n]&...\\ ...&...&...
\end{array} \right]_{N\times N} \end{displaymath}](img240.png)
A symmetric matrix
![]() is positive definite iff
is positive definite iff
![\begin{displaymath}\sum_{m=1}^N \sum_{n=1}^N x[m] a[m,n] y[n] \ge 0,
\;\;\;\mbox{or}\;\;\;\;{\bf x}^T {\bf A} {\bf y}\ge 0 \end{displaymath}](img242.png)
A matrix defines a linear operation, which, when applied to a vector
![]() , generates another vector
, generates another vector ![]() :
:
![\begin{displaymath}\sum_{m=1}^N a[m,n]x[m]=y[m],\;\;\;\;\mbox{or}\;\;\;\;
{\bf A}{\bf x}={\bf y} \end{displaymath}](img245.png)
![\begin{displaymath}\sum_{m=1}^N a[m,n] \phi_i[m] =\lambda_i \phi_i[n],
\;\;\;\;\mbox{or}\;\;\;\; {\bf A} \phi_i=\lambda_i \phi_i \end{displaymath}](img246.png)
![\begin{displaymath}\sum_{n=1}^N \phi_i[n] \phi_j[n] =\delta_{ij},\;\;\;\;\mbox{or}\;\;\;
\phi_i^T \phi_j=\delta_{ij} \end{displaymath}](img247.png)
![\begin{displaymath}a[m,n]=\sum_{i=1}^N \lambda_i \phi_i[m] \phi_j[n] \end{displaymath}](img249.png)