


Next: Appendix B: Kernels and
Up: Appendix A: Conditional and
Previous: Inverse and determinant of
Assume an n-dimensional random vector
has a normal distribution
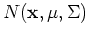 with
with
where 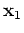 and
and 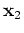 are two subvectors of respective
dimensions
are two subvectors of respective
dimensions 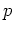 and
and 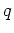 with
with 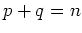 . Note that
. Note that
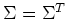 , and
, and
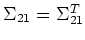 .
.
Theorem 4:
Part a The marginal distributions of 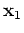 and
and 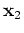 are
also normal with mean vector
are
also normal with mean vector 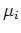 and covariance matrix
and covariance matrix 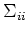 (
(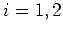 ), respectively.
), respectively.
Part b The conditional distribution of 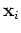 given
given 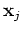 is also normal with mean vector
is also normal with mean vector
and covariance matrix
Proof: The joint density of 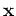 is:
is:
where 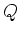 is defined as
is defined as
Here we have assumed
According to theorem 2, we have
Substituting the second expression for 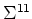 , first expression for
, first expression for 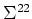 , and
, and 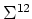 into
into
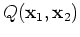 to get:
to get:
The last equal sign is due to the following equations for any vectors
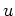 and
and 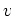 and a symmetric matrix
and a symmetric matrix 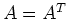 :
:
We define
and
and get
Now the joint distribution can be written as:
The third equal sign is due to theorem 3:
The marginal distribution of 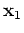 is
is
and the conditional distribution of 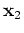 given
given 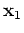 is
is
with



Next: Appendix B: Kernels and
Up: Appendix A: Conditional and
Previous: Inverse and determinant of
Ruye Wang
2006-11-14
![\begin{displaymath}{\bf x}=\left[\begin{array}{c}{\bf x}_1 {\bf x}_2\end{array}\right] \end{displaymath}](img164.png)
![\begin{displaymath}{\bf x}=\left[\begin{array}{c}{\bf x}_1 {\bf x}_2\end{array}\right] \end{displaymath}](img164.png)
![\begin{displaymath}\mu=\left[\begin{array}{c}\mu_1 \mu_2\end{array}\right]\;\...
...1} & \Sigma_{12}\\
\Sigma_{21}&\Sigma_{22}\end{array}\right] \end{displaymath}](img166.png)
![]() and
and ![]() are
also normal with mean vector
are
also normal with mean vector ![]() and covariance matrix
and covariance matrix ![]() (
(![]() ), respectively.
), respectively.
![]() given
given ![]() is also normal with mean vector
is also normal with mean vector
![]() is:
is:
![\begin{displaymath}f({\bf x})=f({\bf x}_1,{\bf x}_2)=\frac{1}{(2\pi)^{n/2\vert\S...
...vert\Sigma\vert^{1/2}}}exp[-\frac{1}{2}Q({\bf x}_1,{\bf x}_2)] \end{displaymath}](img180.png)
![$\displaystyle [({\bf x}_1-\mu_1)^T, ({\bf x}-\mu_2)^T]
\left[\begin{array}{cc}\...
...ght]
\left[\begin{array}{c}{\bf x}_1-\mu_1 {\bf x}_2-\mu_2\end{array}\right]$](img184.png)
![\begin{displaymath}\Sigma^{-1}=\left[\begin{array}{cc}\Sigma_{11} & \Sigma_{12}\...
...} & \Sigma^{12}\\
\Sigma^{21}&\Sigma^{22}\end{array}\right]
\end{displaymath}](img186.png)
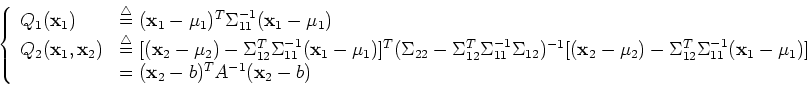
![$\displaystyle f({\bf x}_1,{\bf x}_2)
=\frac{1}{(2\pi)^{n/2\vert\Sigma\vert^{1/2}}}exp[-\frac{1}{2}Q({\bf x}_1,{\bf x}_2)]$](img211.png)
![$\displaystyle \frac{1}{(2\pi)^{n/2}\vert\Sigma_{11}\vert^{1/2} \vert\Sigma_{22}...
...T\Sigma_{11}^{-1}\Sigma_{12}\vert^{1/2}}exp[-\frac{1}{2}Q({\bf x}_1,{\bf x}_2)]$](img212.png)
![$\displaystyle \frac{1}{(2\pi)^{p/2}\vert\Sigma_{11}\vert^{1/2}}exp[-\frac{1}{2}...
...i)^{q/2}\vert A\vert^{1/2}}exp[-\frac{1}{2}({\bf x}_2-b)^T A^{-1}({\bf x}_2-b)]$](img213.png)
![\begin{displaymath}f_1({\bf x}_1)=\int f({\bf x}_1,{\bf x}_2) d{\bf x_2}
=\frac{...
...ac{1}{2}
({\bf x}_1-\mu_1)^T\Sigma_{11}^{-1}({\bf x}_1-\mu_1)]
\end{displaymath}](img216.png)
![\begin{displaymath}f_{2\vert 1}({\bf x}_2\vert{\bf x}_1)=\frac{f({\bf x}_1,{\bf ...
...ert^{1/2}}exp[-\frac{1}{2}({\bf x}_2-b)^T A^{-1}({\bf x}_2-b)]
\end{displaymath}](img217.png)