


Next: Physical Meaning of 1-D
Up: fourier
Previous: Four different forms of
A time signal 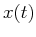 contains the complete information in time domain, i.e., the
amplitude of the signal at any given moment
contains the complete information in time domain, i.e., the
amplitude of the signal at any given moment 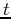 . However, no information is explicitly
available in
. However, no information is explicitly
available in 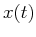 in terms of its frequency contents. On the other hand, the spectrum
in terms of its frequency contents. On the other hand, the spectrum
![$X(f)={\cal F}[x(t)]$](img39.png) of the signal obtained by the Fourier transform (or any other
orthogonal transform such as discrete cosine transform) is extracted from the entire
time duration of the signal, it contains complete information in frequency domain in
terms of the magnitudes and phases of the frequency component at any given frequency
of the signal obtained by the Fourier transform (or any other
orthogonal transform such as discrete cosine transform) is extracted from the entire
time duration of the signal, it contains complete information in frequency domain in
terms of the magnitudes and phases of the frequency component at any given frequency 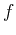 ,
but there is no information explicitly available in the spectrum regarding the temporal
characteristics of the signal, such as when in time certain frequency contents appear.
In this sense, neither
,
but there is no information explicitly available in the spectrum regarding the temporal
characteristics of the signal, such as when in time certain frequency contents appear.
In this sense, neither 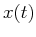 in time domain nor
in time domain nor 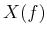 in frequency domain provides
complete description of the signal. In other words, we can have either temporal or
spectral locality regarding the information contained in the signal, but never both.
in frequency domain provides
complete description of the signal. In other words, we can have either temporal or
spectral locality regarding the information contained in the signal, but never both.
- The short-time Fourier transform (STFT), also called windowed
Fourier transform, can be used to address this dilemma. The signal
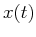 to be
Fourier analyzed is first truncated by a time window function
to be
Fourier analyzed is first truncated by a time window function 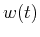 which is
zero outside a certain time interval
which is
zero outside a certain time interval 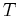 , such as a square or Gaussian window,
before it is transformed to the frequency domain. Now any characteristics appearing
in the spectrum will be known to be from within this particular time window. In time
domain, the windowed signal is:
, such as a square or Gaussian window,
before it is transformed to the frequency domain. Now any characteristics appearing
in the spectrum will be known to be from within this particular time window. In time
domain, the windowed signal is:
According to convolution theorem, this equation corresponds to the following in
frequency domain:
where
![$X_w(f)={\cal F}[x_w(t)]$](img44.png) and
and
![$W(f)={\cal F}[ w(t) ]$](img45.png) are the spectra of
are the spectra of 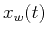 and
and 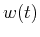 , respectively. Now we know that all frequency components present in the
spectrum
, respectively. Now we know that all frequency components present in the
spectrum 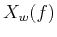 exist inside the time window, and the narrower the time window, the
better the temporal resolution. However, on the other hand, the spectrum
exist inside the time window, and the narrower the time window, the
better the temporal resolution. However, on the other hand, the spectrum 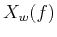 of
the windowed signal is a blurred version of the true signal spectrum
of
the windowed signal is a blurred version of the true signal spectrum 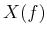 , due to
the convolution with the spectrum
, due to
the convolution with the spectrum 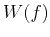 of the window. Moreover, we see that while
the temporal resolution can be increased by a narrow window
of the window. Moreover, we see that while
the temporal resolution can be increased by a narrow window 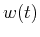 , the frequency
resolution will be reduced due to the expanded spectrum
, the frequency
resolution will be reduced due to the expanded spectrum 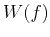 . Similarly, a narrower
. Similarly, a narrower
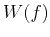 for better frequency resolution corresponds to a wider window causing poorer
temporal resolution.
for better frequency resolution corresponds to a wider window causing poorer
temporal resolution.
- Fourier series expansion. If we assume the windowed signal repeats itself
outside the window, i.e., it becomes a periodic signal with period
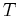 . The
spectrum of this periodic signal is discrete, weighted by the Fourier coefficients,
with a gap
. The
spectrum of this periodic signal is discrete, weighted by the Fourier coefficients,
with a gap 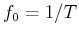 , the fundamental frequency, between every two consecutive
frequency components, i.e.,
, the fundamental frequency, between every two consecutive
frequency components, i.e.,
This relationship indicates that it is impossible to increase both the temporal
resolution (reduced 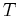 ) and the frequency resolution (reduced
) and the frequency resolution (reduced 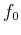 ). When one
of the resolutions is improved, the other must suffer.
). When one
of the resolutions is improved, the other must suffer.
- The uncertainty principle describes the general phenomenon quantitatively,
similar to the Heisenberg Uncertainty Principle in quantum physics which
states that it is impossible to precisely measure both the position and momentum
of a microscopic particle at the same time. The more precisely one of the quantities
is measured, the less precisely the other is known.
To show this, we borrow the concept of probability density function (PDF) from
the probability theory. Any given time signal 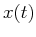 can be treated as a PDF by
normalization:
can be treated as a PDF by
normalization:
where the denominator is the total energy of the signal 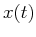 assumed to be
finite; i.e.,
assumed to be
finite; i.e., 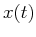 is an energy signal. As
is an energy signal. As 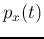 satisfies these conditions
satisfies these conditions
How the signal 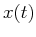 spreads over time; i.e., the locality or the dispersion
of
spreads over time; i.e., the locality or the dispersion
of 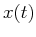 , can be measured as the variance of this probability density
, can be measured as the variance of this probability density 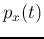 :
:
where 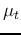 is the mean of
is the mean of 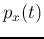 :
:
Similarly, in the frequency domain, the locality or dispersion of the spectrum
of the signal can also be measured as
Here, we have used Parseval's identity
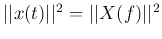 , and
, and 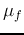 is
defined as
is
defined as
The uncertainty principle:
Let
![$X(f)={\cal F}[x(t)]$](img39.png) be the Fourier spectrum of a given function
be the Fourier spectrum of a given function 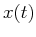 and
and 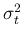 and
and 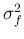 be defined as above. Then
be defined as above. Then



Next: Physical Meaning of 1-D
Up: fourier
Previous: Four different forms of
Ruye Wang
2015-11-12
![]() contains the complete information in time domain, i.e., the
amplitude of the signal at any given moment
contains the complete information in time domain, i.e., the
amplitude of the signal at any given moment ![]() . However, no information is explicitly
available in
. However, no information is explicitly
available in ![]() in terms of its frequency contents. On the other hand, the spectrum
in terms of its frequency contents. On the other hand, the spectrum
![]() of the signal obtained by the Fourier transform (or any other
orthogonal transform such as discrete cosine transform) is extracted from the entire
time duration of the signal, it contains complete information in frequency domain in
terms of the magnitudes and phases of the frequency component at any given frequency
of the signal obtained by the Fourier transform (or any other
orthogonal transform such as discrete cosine transform) is extracted from the entire
time duration of the signal, it contains complete information in frequency domain in
terms of the magnitudes and phases of the frequency component at any given frequency ![]() ,
but there is no information explicitly available in the spectrum regarding the temporal
characteristics of the signal, such as when in time certain frequency contents appear.
In this sense, neither
,
but there is no information explicitly available in the spectrum regarding the temporal
characteristics of the signal, such as when in time certain frequency contents appear.
In this sense, neither ![]() in time domain nor
in time domain nor ![]() in frequency domain provides
complete description of the signal. In other words, we can have either temporal or
spectral locality regarding the information contained in the signal, but never both.
in frequency domain provides
complete description of the signal. In other words, we can have either temporal or
spectral locality regarding the information contained in the signal, but never both.
![]() can be treated as a PDF by
normalization:
can be treated as a PDF by
normalization:
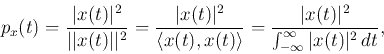
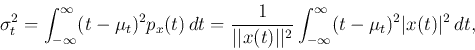
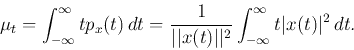
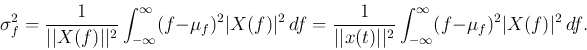
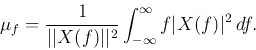
![]() be the Fourier spectrum of a given function
be the Fourier spectrum of a given function ![]() and
and ![]() and
and ![]() be defined as above. Then
be defined as above. Then