Four different forms of the Fourier transform

• Non-periodic, continuous time function $x(t)$, continuous, non-periodic spectrum $X(f)$

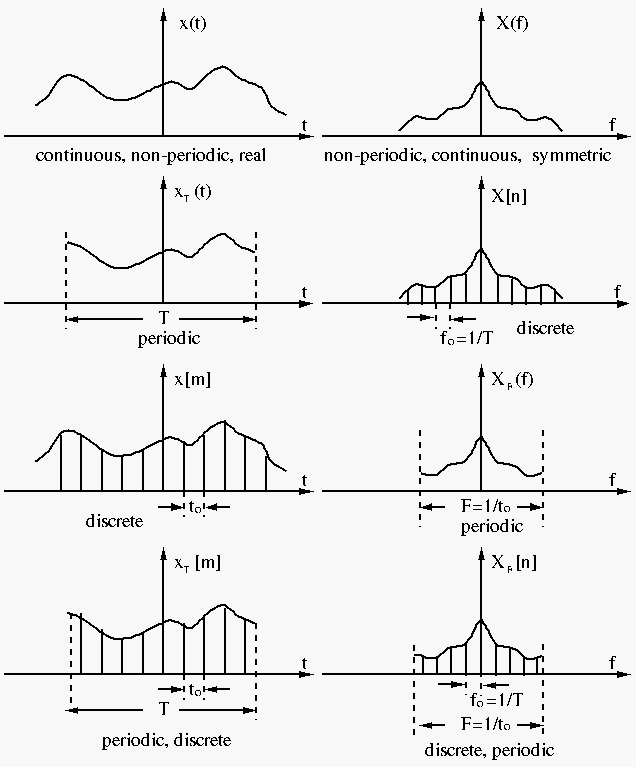
  This is the most general form of Fourier transform.
  

  $$X(f)=\int_{-\infty}^{\infty} x(t) e^{-j2\pi ft} dt,\;\;\;\;\; x(t)=\int_{-\infty}^{\infty} X(f) e^{j2\pi ft} df$$
  
  
  Alternatively, as $\omega=2\pi f$, we have
  
  $$X(\omega)=\int_{-\infty}^{\infty} x(t) e^{-j\omega t} dt,\;\;... ...}{2\pi}\int_{-\infty}^{\infty} X(\omega) e^{j\omega t} d\omega$$
  
  

  The first one is the forward transform, and the second one is the inverse transform.

• Non-periodic, discrete time function $x[n]$, continuous, periodic spectrum $X_F (f)$

  The discrete time function can be considered as a sequence of samples of continuous time function. The time interval between two consecutive samples $x[m]$ and $x[m+1]$ is $t_0=1/F$, where $F$ is the sampling rate, which is also the period of the spectrum in the frequency domain.

  The discrete time function can be written as
  

  $$x(t)=\sum_{m=-\infty}^{\infty} x[m]\delta(t-mt_0)$$
  
  

  and its transform is:

  
  

  $$X_F(f)=\sum_{m=-\infty}^{\infty} x[m]e^{-j2\pi fmt_0},\;\;\;\... ... x[m]=\frac{1}{F} \int_{-F/2}^{+F/2} X_F(f) e^{j2\pi fmt_0} df$$
  
  
  
  
  $$(m=0, \pm 1, \pm 2, \cdots)$$
  
  

  We can verify that the spectrum is indeed periodic:
  

  $$X_F(f+kF)=X_F(f+k/t_0)=\sum_{m=-\infty}^{\infty} x[m]e^{-j2\pi (f+k/t_0)mt_0}=X_F(f)$$
  
  
  (for $k=\pm 1, \pm 2, \cdots$) because $e^{\pm j2\pi mk} =1$.

• Periodic, continuous time function $x_T(t)$, discrete, non-periodic spectrum $X[n]$

  This is the Fourier series expansion of periodic functions. The time period is $T$, and the interval between two consecutive frequency components is $f_0=1/T$, and its transform is:
  

  $$X[n]=\frac{1}{T} \int_T x_T(t) e^{-j2\pi nf_0t} dt,\;\;\;\;\;\; x_T(t)=\sum_{n=-\infty}^{\infty} X[n]e^{j2\pi nf_0t}$$
  
  
  
  
  $$n=0, \pm 1, \pm 2, \cdots$$
  
  

  The discrete spectrum can also be represented as:
  

  $$X(f)=\sum_{n=-\infty}^{\infty} X[n]\delta(f-nf_0)$$
  
  

  We can verify that the time function is indeed periodic:
  

  $$x_T(t+kT)=x_T(t+k/f_0)=\sum_{n=-\infty}^{\infty} X[n]e^{-j2\pi nf_0(t+k/f_0)}=x_T(t)$$
  
  
  (for $k=\pm 1, \pm 2, \cdots$)

  

• Periodic, discrete time function $x[m]$, discrete, periodic spectrum $X[n]$

  This is the discrete Fourier transform (DFT).

  
  

  $$X[n]=\frac{1}{T}\sum_{m=0}^{N-1} x[m]e^{-j2\pi nmf_0t_0},\;\;\;\;\;\; x[m]=\frac{1}{F}\sum_{n=0}^{N-1} X[n]e^{j2\pi nmf_0t_0}$$
  
  
  
  
  $$m,n=0, 1, \cdots, N-1$$
  
  
  Here $N$ is the number of samples in the period $T$, which is also the number of frequency components in the spectrum:
  
  $$N=\frac{T}{t_0}=\frac{1/f_0}{1/F}=\frac{F}{f_0}$$
  
  
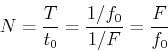
  We therefore also have $TF=N$ and $t_0f_0=1/N$.

  The DFT can be redefined as

  
  

  $$X[n]=\frac{1}{\sqrt{N}}\sum_{m=0}^{N-1} x[m]e^{-mn j2\pi/N} ... ...0}^{N-1} X[n]e^{mn j2\pi/N} =\sum_{n=0}^{N-1} w_N^{-mn} X[n]$$
  
  
  
  
  $$m,n=0, 1, \cdots, N-1$$
  
  

  where $w_N\stackrel{\triangle}{=}e^{-j2\pi/N}/\sqrt{N}$.

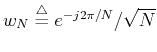  We can easily verify that the time function and its spectrum are indeed periodic: $x[m+kN]=x[m]$ and $X[n+kN]=X[n]$.

  Note that there are alternative ways for arranging the constant coefficients. For example, one could define the forward transform without the coefficient $1/\sqrt{N}$, and have $1/N$ as the coefficient for the inverse transform.