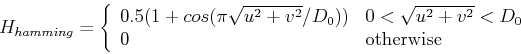Next: About this document ...
Up: fourier
Previous: Fourier Filtering 1D
In the spatial frequency domain, the spectrum of the 2D spatial signal (the
image) is represented by a 2D array
![$X[k,l]=X_r[k,l]+j X_i[k,l]$](img331.png) . An arbitrary
location
. An arbitrary
location 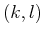 in the spectrum array represents a spatial sinusoid with
in the spectrum array represents a spatial sinusoid with
- frequency
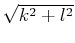 and
and
- direction
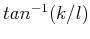
And the complex coefficient
![$X[k,l]=X_r[k,l]+jX_i[k,j]$](img335.png) specifies the
specifies the
- magnitude
![$\sqrt{X_r[k,l]^2+X_i[k,l]^2}$](img336.png) , and
, and
- phase angle
![$tan^{-1}(X_i[k,l]/X_r[k,l])$](img337.png)
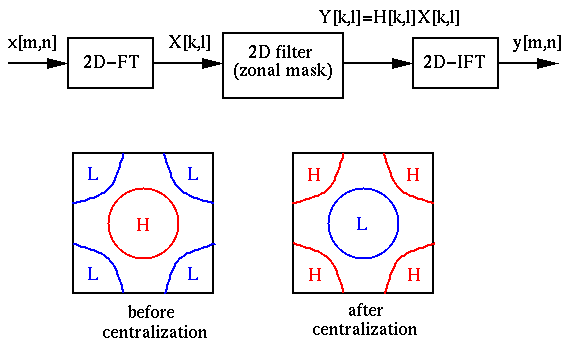
of the sinusoid. All frequency components ![$X[k,l]$](img227.png) can be modified according
to specific filtering needs. We could enhance and/or reduce various frequency
components by multiplying the spectrum by a 2D filter mask. Note that if the
spectrum is centralized, the DC is in the middle
can be modified according
to specific filtering needs. We could enhance and/or reduce various frequency
components by multiplying the spectrum by a 2D filter mask. Note that if the
spectrum is centralized, the DC is in the middle 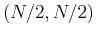 of the spectrum.
The farther a frequency component
of the spectrum.
The farther a frequency component 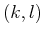 is from this point, the higher
frequency it has.
is from this point, the higher
frequency it has.
Here are some typical 2D filters. We assume
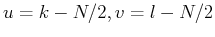 in the
following.
in the
following.
- Ideal low-pass filter
where 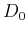 is the ideal cut-off frequency.
is the ideal cut-off frequency.
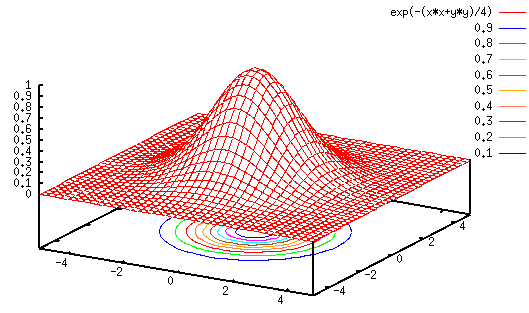
- Gaussian low-pass filter
where 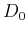 is the cut-off frequency at which (
is the cut-off frequency at which (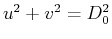 )
the magnitude is attenuated to
)
the magnitude is attenuated to 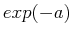 , and
, and 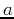 and
and 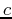 are two
parameters. Compared with the ideal filter, the Gaussian filter is
smooth and it no longer have the undesired ringing effect.
are two
parameters. Compared with the ideal filter, the Gaussian filter is
smooth and it no longer have the undesired ringing effect.
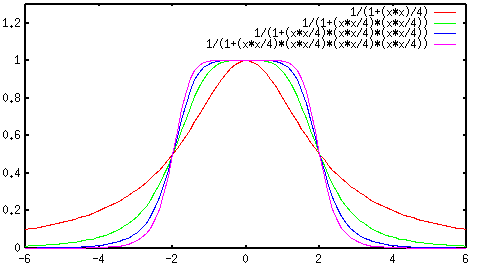
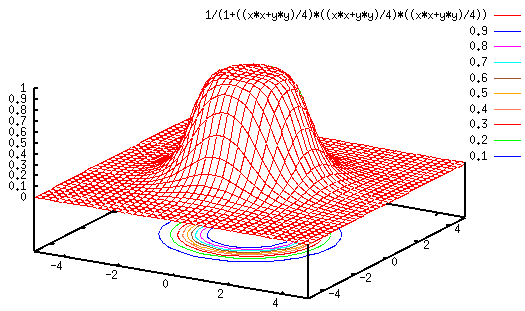
- Butterworth low-pass filter
Butterworth filter is also a smooth low-pass filter with a parameter 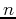 .
Note that when
.
Note that when
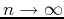 , the Butterworth filter becomes an
ideal filter.
, the Butterworth filter becomes an
ideal filter.
- Hamming low-pass filter
The high-pass filters corresponding to each of the low-pass filters above
can be obtained by
Alternatively, the same filters above can be used as high-pass filters if
they are applied to the 2D spectrum without centralization.
The filtering effects are shown in these
demonstrations



Next: About this document ...
Up: fourier
Previous: Fourier Filtering 1D
Ruye Wang
2015-11-12
![]() . An arbitrary
location
. An arbitrary
location ![]() in the spectrum array represents a spatial sinusoid with
in the spectrum array represents a spatial sinusoid with
![$\sqrt{X_r[k,l]^2+X_i[k,l]^2}$](img336.png) , and
, and

![]() in the
following.
in the
following.
![\begin{displaymath}H_{ideal}[k,l]=\left\{ \begin{array}{ll}
1 & \sqrt{u^2+v^2} <D_0 \\
0 & \mbox{otherwise} \end{array} \right. \end{displaymath}](img340.png)

![\begin{displaymath}H_{butterworth}[k,l]=\frac{1}{1+((u^2+v^2)/D_0^2)^n}
=\left...
...u^2+v^2=D_0^2 0 & u,v\rightarrow \infty \end{array} \right. \end{displaymath}](img347.png)