


Next: About this document ...
Up: dct
Previous: Definition of DCT
Forward DCT
The DCT of a sequence
![$\{x[m],\;\;\;(m=0,\cdots,N-1)\;\}$](img61.png) can be implemented by
FFT. First we define a new sequence
can be implemented by
FFT. First we define a new sequence
![$\{\;y[m],\;\;\;(m=0,\cdots,N-1)\;\}$](img62.png) :
:
Then the DCT of ![$x[n]$](img64.png) can be written as the following (the coefficient
can be written as the following (the coefficient ![$a[n]$](img41.png) is dropped for now for simplicity):
is dropped for now for simplicity):
where the first summation is for all even terms and second all odd terms. We define
for the second summation
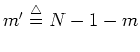 , then the limits of the
summation
, then the limits of the
summation 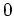 and
and 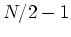 for
for 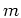 becomes
becomes 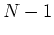 and
and 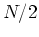 for
for 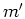 , and the second
summation can be written as
, and the second
summation can be written as
Now the two summations in the expression of ![$X[n]$](img33.png) can be combined
can be combined
Next, consider the DFT of ![$y[m]$](img75.png) :
:
If we multiply both sides by
and take the real part of the result (and keep in mind that both ![$x[m]$](img12.png) and
and ![$y[m]$](img75.png) are real), we get:
are real), we get:
The last equal sign is due to the trigonometric identity:
This expression for
![$Re[e^{-jn\pi/2N} Y[n]]$](img80.png) is identical to that for
is identical to that for ![$X[n]$](img33.png) above,
therefore we get
above,
therefore we get
where ![$Y[n]$](img82.png) is the DFT of
is the DFT of ![$y[m]$](img75.png) (defined from
(defined from ![$x[m]$](img12.png) ) which can be
computed using FFT algorithm with time complexity
) which can be
computed using FFT algorithm with time complexity 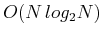 .
.
In summary, fast forward DCT can be implemented in 3 steps:
- Step 1: Generate a sequence
![$y[m]$](img75.png) from the given sequence
from the given sequence ![$x[m]$](img12.png) :
:
- step 2: Obtain DFT
![$Y[n]$](img82.png) of
of ![$y[m]$](img75.png) using FFT. (As
using FFT. (As ![$y[m]$](img75.png) is real,
is real,
![$Y[n]$](img82.png) is symmetric and only half of the data points need be computed.)
is symmetric and only half of the data points need be computed.)
- step 3: Obtain DCT
![$X[n]$](img33.png) from
from ![$Y[n]$](img82.png) by
by
Inverse DCT
The most obvious way to do inverse DCT is to reverse the order and the
mathematical operations of the three steps for the forward DCT:
However, there is a more efficient way to do the inverse DCT. Consider first
the real part of the inverse DFT of the sequence
![$X[n]e^{jn\pi/2N}$](img91.png) :
:
This equation gives the inverse DCT of all 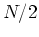 even data points
even data points
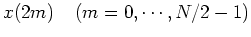 . To obtain the odd data points, recall
that
. To obtain the odd data points, recall
that
![$x[m]=x[2N-m-1]$](img94.png) , and all odd data points
, and all odd data points
can be obtained from the second half of the previous equation in reverse
order
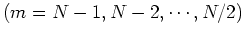 .
.
In summary, we have these steps to compute IDCT:
- step 1: Generate a sequence
![$Y[n]$](img82.png) from the given DCT sequence
from the given DCT sequence
![$X[n]$](img33.png) :
:
- step 2: Obtain
![$y[m]$](img75.png) from
from ![$Y[n]$](img82.png) by inverse DFT also using FFT.
(Only the real part need be computed.)
by inverse DFT also using FFT.
(Only the real part need be computed.)
- Step 3: Obtain
![$x[m]'s$](img99.png) from
from ![$y[m]'s$](img86.png) by
by
These three steps are mathematically equivalent to the steps of the first
method.
See the demos.



Next: About this document ...
Up: dct
Previous: Definition of DCT
Ruye Wang
2013-10-27
![]() can be implemented by
FFT. First we define a new sequence
can be implemented by
FFT. First we define a new sequence
![]() :
:
![\begin{displaymath}\left\{ \begin{array}{ll} y[m]\stackrel{\triangle}{=}x[2m] & ...
...triangle}{=}x[2m+1] & (i=0,\cdots, N/2-1) \end{array} \right.
\end{displaymath}](img63.png)
![$\displaystyle \sum_{m=0}^{N-1} x[m] \cos\left( \frac{ (2m+1)n\pi}{2N}\right)$](img65.png)
![$\displaystyle \sum_{m=0}^{N/2-1}x[2m] \cos\left( \frac{ (4m+1)n\pi}{2N} \right) +
\sum_{m=0}^{N/2-1}x[2m+1] \cos\left( \frac{ (4m+3)n\pi}{2N} \right)$](img66.png)
![$\displaystyle \sum_{m=0}^{N/2-1}y[m] \cos\left( \frac{ (4m+1)n\pi}{2N} \right)+
\sum_{m=0}^{N/2-1}y[N-1-m] \cos\left( \frac{ (4m+3)n\pi}{2N}\right)$](img67.png)
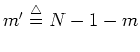 , then the limits of the
summation
, then the limits of the
summation ![\begin{displaymath}
\sum_{m'=N/2}^{N-1} y[m'] \cos\left( 2n\pi - \frac{ (4m'+1)...
...m'=N/2}^{N-1} y[m'] \cos\left( \frac{ (4m'+1)n\pi}{2N} \right)
\end{displaymath}](img73.png)
![\begin{displaymath}X[n]=\sum_{m=0}^{N-1}y[m] \cos\left( \frac{ (4m+1)n\pi}{2N}\right) \end{displaymath}](img74.png)
![]() :
:
![\begin{displaymath}
Y[n]=\sum_{m=0}^{N-1} y[m] e^{-j2\pi mn/N}
=\sum_{m=0}^{N-1...
...i mn}{N}\right)-j\;\sin\left(\frac{2\pi mn}{N}\right) \right]
\end{displaymath}](img76.png)
![\begin{displaymath}
Re[e^{-jn\pi/2N} Y[n]]=\sum_{m=0}^{N-1} y[m] \left[\cos\left...
...sum_{m=0}^{N-1} y[m] \cos\left( \frac{ (4m+1)n\pi}{2N} \right)
\end{displaymath}](img78.png)
![\begin{displaymath}\left\{ \begin{array}{ll} y[m]=x[2m] & \\
y[N-1-m]=x[2m+1] & (i=0,\cdots, N/2-1) \end{array} \right.
\end{displaymath}](img84.png)
![\begin{displaymath}\left\{ \begin{array}{ll} x[2m]=y[m] & \\
x[2m+1]=y[N-1-m] & (i=0,\cdots, N/2-1) \end{array} \right.
\end{displaymath}](img90.png)
![]() :
:
![\begin{displaymath}
Re\;\left[ \sum_{n=0}^{N-1} [X[n]e^{jn\pi/2N}]\;e^{j2\pi mn...
...4m+1)n\pi}{2N}\right)
= x[2m]\;\;\;\;\;\;(m=0, \cdots, N-1)
\end{displaymath}](img92.png)
![\begin{displaymath}\left\{ \begin{array}{ll} x[2m]=y[m] & \\
x[2m+1]=y[N-1-m] & (i=0,\cdots, N/2-1) \end{array} \right.
\end{displaymath}](img90.png)