


Next: Fast DCT algorithm
Up: dct
Previous: dct
The discrete Fourier transform (DFT) transforms a complex signal into its
complex spectrum. However, if the signal is real as in most of the applications,
half of the data is redundant. In time domain, the imaginary part of the signal
is all zero; in frequency domain, the real part of the spectrum is even symmetric
and imaginary part odd. In comparison, Discrete cosine transform (DCT) transforms
is a real transform that transforms a sequence of real data points into its real
spectrum and therefore avoids the problem of redundancy. Also, as DCT is derived
from DFT, all the desirable properties of DFT (such as the fast algorithm) are
preserved.
To derive the DCT of an N-point real signal sequence
![$\{x[0],\cdots,x[N-1]\}$](img1.png) ,
we first construct a new sequence of
,
we first construct a new sequence of 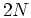 points:
points:
This 2N-point sequence ![$x'[m]$](img4.png) is assumed to repeat its self outside the range
is assumed to repeat its self outside the range
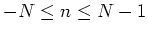 , i.e., it is periodic with period
, i.e., it is periodic with period 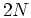 , and it is even
symmetric with respect to the point at
, and it is even
symmetric with respect to the point at 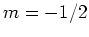 :
:
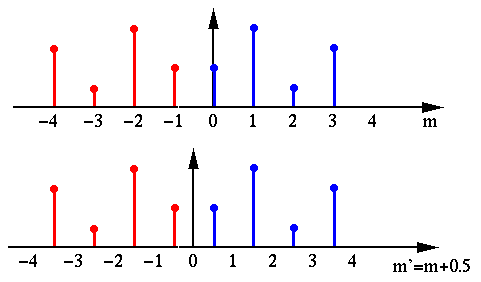
If we shift the points ![$x'[m]$](img4.png) to the right by 1/2, or, equivalently,
shift
to the right by 1/2, or, equivalently,
shift 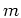 to the left by 1/2 by defining another index
to the left by 1/2 by defining another index 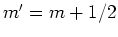 , then
, then
![$x'[m]=x'[m'-1/2]$](img10.png) is even symmetric with respect to the origin at
is even symmetric with respect to the origin at 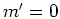 .
In the following we simply represent this new function by
.
In the following we simply represent this new function by ![$x[m]$](img12.png) .
.
The DFT of this 2N-point even symmetric sequence can be found as:
Here we have used the fact that ![$x[m'-1/2]$](img18.png) is even,
is even,
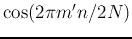 and
and
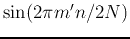 are respectively even and odd, all with respect to
are respectively even and odd, all with respect to  or
or  . Consequently the first summation of all even terms is twice that
with half of the range
. Consequently the first summation of all even terms is twice that
with half of the range
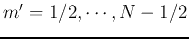 , while the second summation of all
odd terms is zero. Replacing
, while the second summation of all
odd terms is zero. Replacing 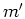 by
by 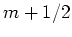 , we get the discrete cosine transform
(DCT):
, we get the discrete cosine transform
(DCT):
where the coefficient ![$c[n,m]$](img26.png) defined as
defined as
which can be considered as the component on the mth row and nth column of an 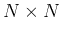 matrix
matrix 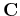 , called the DCT matrix.
, called the DCT matrix.
As ![$X[n]=X[-n]$](img30.png) is even and of period
is even and of period 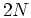 , we further have
, we further have
i.e., the second 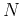 coefficients
coefficients ![$X[n]$](img33.png) for
for
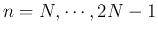 are redundant and
can be dropped. Now the the range for index
are redundant and
can be dropped. Now the the range for index 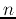 is reduced to
is reduced to
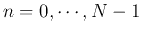 .
We can show that all row vectors of
.
We can show that all row vectors of 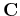 are orthogonal and normalized, except
the first one (
are orthogonal and normalized, except
the first one (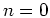 ):
):
To make DCT a orthonormal transform, we define a coefficient
so that the DCT now becomes
where ![$c[n,m]$](img26.png) is modified with
is modified with ![$a[n]$](img41.png) , which is also the component in the nth
row and mth column of the N by N cosine transform matrix:
, which is also the component in the nth
row and mth column of the N by N cosine transform matrix:
Here
![${\bf c}_i^T=[c[i,0],\cdots,c[i,N-1]$](img43.png) is the ith row of the DCT transform
matrix
is the ith row of the DCT transform
matrix 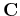 . As these row vectors are orthogonal:
. As these row vectors are orthogonal:
the DCT matrix 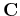 is orthogonal:
is orthogonal:
and it is real
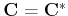 . Now the DCT can be expressed in matrix form as:
. Now the DCT can be expressed in matrix form as:
Left multiplying both sides by 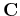 we get
we get
this is the inverse DCT:
or in component form:
Example: When 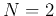 , we have
, we have
![$c[n,m]=a[n]\cos((2m+1)n\pi/4)$](img52.png) for
for 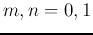 , and
, and
An 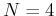 -point DCT matrix can be generated by
-point DCT matrix can be generated by
![$c[n,m]=a[n] cos( (2m+1)n\pi/8)$](img56.png) to be
to be
Assume the signal is
![${\bf x}=[0\; 1\; 2\; 3]^T$](img58.png) , then its DCT transform is:
, then its DCT transform is:
The inverse transform is:
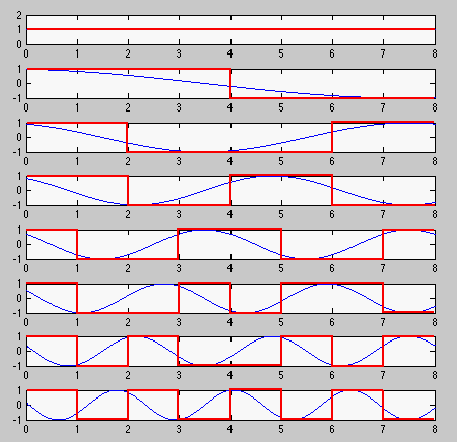
This result is very similar to the example shown in the previous section for
WHT transform. In fact, these two transforms are very comparable, as seen from
the figure below:
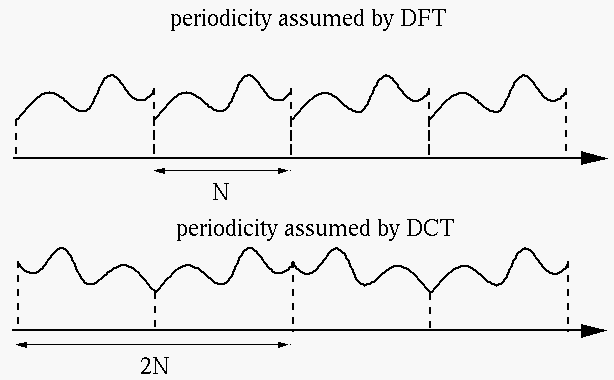
Compared with DFT, DCT has two main advantages:
- It is a real transform with better computational efficiency than DFT
which by definition is a complex transform.
- It does not introduce discontinuity while imposing periodicity in the
time signal. In DFT, as the time signal is truncated and assumed periodic,
discontinuity is introduced in time domain and some corresponding artifacts
is introduced in frequency domain. But as even symmetry is assumed while
truncating the time signal, no discontinuity and related artifacts are
introduced in DCT.



Next: Fast DCT algorithm
Up: dct
Previous: dct
Ruye Wang
2013-10-27
![]() ,
we first construct a new sequence of
,
we first construct a new sequence of ![]() points:
points:
![\begin{displaymath}x'[m]\stackrel{\triangle}{=}\left\{ \begin{array}{ll}
x[m] ...
...\leq N-1) x[-m-1] & (-N \leq m \leq -1)
\end{array} \right. \end{displaymath}](img3.png)

![$\displaystyle \frac{1}{\sqrt{2N}} \sum_{m'=-N+1/2}^{N-1/2} x\left[m'-\frac{1}{2}\right]e^{-j2\pi m'n/2N}$](img15.png)
![$\displaystyle \frac{1}{\sqrt{2N}} \sum_{m'=-N+1/2}^{N-1/2}x\left[m'-\frac{1}{2}...
...+1/2}^{N-1/2}x\left[m'-\frac{1}{2}\right]\;\sin\left(\frac{2\pi m'n}{2N}\right)$](img16.png)
![$\displaystyle \frac{1}{\sqrt{2N}} \sum_{m'=-N+1/2}^{N-1/2}x\left[m'-\frac{1}{2}...
...2}\right]\;\cos\left(\frac{2\pi m'n}{2N}\right)
\;\;\;\;\;\;\;(n=0,\cdots,2N-1)$](img17.png)
![$\displaystyle \sqrt{\frac{2}{N}} \sum_{m'=1/2}^{N-1/2}x\left[m'-\frac{1}{2}\rig...
...\sqrt{\frac{2}{N}} \sum_{m=0}^{N-1}x[m]\;\cos\left(\frac{(2m+1)n\pi}{2N}\right)$](img24.png)
![$\displaystyle \sum_{m=0}^{N-1} c[n,m]x[m],\;\;\;\;\;\;\;\;\;(n=0,\cdots,N-1)$](img25.png)
![\begin{displaymath}
c[n,m]\stackrel{\triangle}{=}\sqrt{\frac{2}{N}}\cos\left(\frac{ (2m+1)n\pi}{2N}\right),
\;\;\;\;\;\;\;(m,n=0,1,\cdots,N-1)
\end{displaymath}](img27.png)
![]() is even and of period
is even and of period ![]() , we further have
, we further have
![\begin{displaymath}\sqrt{\sum_{m=0}^{N-1}c^2[n,m]}=
\sqrt{\frac{2}{N} \sum_{m=0}...
...qrt{2} &\;\;n=0 1 &\;\;n=1,2,\cdots,N-1
\end{array} \right. \end{displaymath}](img38.png)
![\begin{displaymath}a[n]=\left\{ \begin{array}{ll} \sqrt{1/N} & \;\;n=0 \sqrt{2/N} &\;\;
n=1,2,\cdots,N-1 \end{array} \right.
\end{displaymath}](img39.png)
![\begin{displaymath}X[n] = a[n] \sum_{m=0}^{N-1}x[m]\;\cos\left(\frac{ (2m+1)n\pi...
...)
=\sum_{m=0}^{N-1}x[m]\;c[n,m]\;\;\;\;\;\;\;(n=0,\cdots,N-1)
\end{displaymath}](img40.png)
![\begin{displaymath}
\left[ \begin{array}{ccc} \cdots & \cdots & \cdots \\
\vdot...
...T \vdots {\bf c}_{N-1}^T \end{array} \right]
={\bf C}^T
\end{displaymath}](img42.png)
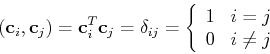
![\begin{displaymath}x[m] = \sum_{n=0}^{N-1} X[n]\;c[m,n]=
\sum_{n=0}^{N-1} a[n] X...
...t)
=\sum_{n=0}^{N-1}X[n]\;c[n,m]\;\;\;\;\;\;\;(m=0,\cdots,N-1) \end{displaymath}](img50.png)
![]() , we have
, we have
![]() for
for ![]() , and
, and
![\begin{displaymath}{\bf C}=\frac{1}{\sqrt{2}}\left[\begin{array}{cr} 1 & 1 1 & -1\end{array}\right] \end{displaymath}](img54.png)
![\begin{displaymath}{\bf C}^T=\left[ \begin{array}{c} {\bf c}_0^T \vdots {\...
....50 & 0.50 \\
0.27 & -0.65 & 0.65 & -0.27 \end{array} \right] \end{displaymath}](img57.png)
![\begin{displaymath}{\bf X}={\bf C}^T {\bf x}=\left[ \begin{array}{rrrr}
0.50 & ...
...egin{array}{r} 3.00 -2.23 0.00 -0.16 \end{array} \right] \end{displaymath}](img59.png)
![\begin{displaymath}{\bf x}={\bf C} {\bf X}=\left[ \begin{array}{rrrr}
0.50 & 0....
...ht]
=\left[ \begin{array}{r} 0 1 2 3 \end{array} \right] \end{displaymath}](img60.png)

