Gray Level Image Compression

Bit-plane decomposition:

The $2^n=N$ gray levels of the image can be represented by

$$G=\sum_{i=0}^{n-1} b_i 2^i,\;\;\;\;\;0 \le G \le 2^n-1,\;\;\;\;b_i=0,1$$

An image of $N$ (e.g., $N=256$) gray levels can be decomposed into a set of $n=log_2 N$ (e.g., $n=8$) binary images which can be compressed using the binary image compression methods.

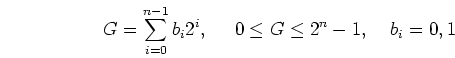
For better compression result, it is desirable for the sequences of consecutive 1's or 0's in the binary images to be as long as possible. However, one problem one may encounter is that the values of many of the bit planes may change, even though the gray level of the n-bit image changes very little, such as in a smooth region of the image.

Example:

$$\begin{tabular}{c\vert l} \hline $127 \rightarrow 128$ & $... ...64$ & $00111111 \rightarrow 01000000$ \hline \end{tabular}$$

In these cases, a minor change in gray level image will cause many bit-planes to change.

To improve, the binary coding of the N gray levels can be converted to Gray code which guarantees only one of the bit plane will change when the gray level changes continuously.

$$\begin{tabular}{l\vert\vert l\vert l\vert l\vert l\vert l\ver... ...01 & 011 & 010 & 110 & 111 & 101 & 100 \hline \end{tabular}$$

$$g_i=b_i \oplus b_{i+1},\;\;\;\; i=0,1,\cdots,n,\;\;\;\;b_n=0$$