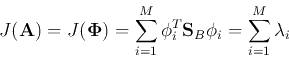Next: Optimal transformation for maximizing
Up: Feature Selection
Previous: Feature Selection
First we realize that the separability criterion
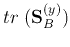 in the
space
in the
space
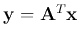 can be expressed as:
can be expressed as:
The optimal transform matrix 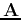 which maximizes
which maximizes
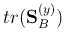 can be
obtained by solving the following optimization problem:
can be
obtained by solving the following optimization problem:
Here we have further assumed that 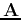 is an orthogonal matrix (a justifiable
constraint as orthogonal matrices conserve energy/information in the signal
vector). This constrained optimization problem can be solved by Lagrange
multiplier method:
is an orthogonal matrix (a justifiable
constraint as orthogonal matrices conserve energy/information in the signal
vector). This constrained optimization problem can be solved by Lagrange
multiplier method:
We see that the column vectors of 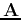 must be the orthogonal eigenvectors of
the symmetric matrix
must be the orthogonal eigenvectors of
the symmetric matrix 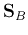 :
:
i.e., the transform matrix must be
Thus we have proved that the optimal feature selection transform is the
principal component transform (KLT) which, as we have shown before, tends to
compact most of the energy/information (representing separability here) into
a small number of components. Therefore the 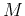 new features can be obtained by
new features can be obtained by
and
Obviously, to maximize  , we just need to choose the
, we just need to choose the 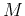 eigenvectors
eigenvectors
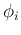 's corresponding to the
's corresponding to the 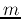 largest eigenvalues of
largest eigenvalues of 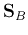 :
:
In the subspace spanned by these 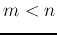 new features,
new features, 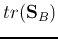 with be
maximized.
with be
maximized.



Next: Optimal transformation for maximizing
Up: Feature Selection
Previous: Feature Selection
Ruye Wang
2016-11-30
![]() in the
space
in the
space
![]() can be expressed as:
can be expressed as:
![$\displaystyle tr\;({\bf S}_{B}^{(y)}) = tr\;({\bf A}^T {\bf S}_{B}^{(x)} {\bf...
...s {\bf a}_N^T\end{array} \right]{\bf S}_B^{(x)}[{\bf a}_1,\cdots,{\bf a}_N]$](img379.png)
![$\displaystyle tr \; \left[ \begin{array}{c} {\bf a}_1^T \vdots {\bf a}_N...
...{\bf S}_{B}^{(x)}{\bf a}_N]
=\sum_{i=1}^N {\bf a}_i^T{\bf S}_B^{(x)}{\bf a}_i$](img380.png)
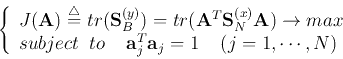
![$\displaystyle \frac{\partial}{\partial {\bf a}_i}\left[J({\bf A})-\sum_{j=1}^N ...
...}_j^T{\bf S}_B^{(x)}{\bf a}_j-\lambda_j {\bf a}_j^T{\bf a}_j+\lambda_j) \right]$](img383.png)
![$\displaystyle \frac{\partial}{\partial {\bf a}_i}
\left[{\bf a}_i^T{\bf S}_B^{...
...\bf a}_i^T{\bf a}_i \right]
= 2{\bf S}_B^{(x)}{\bf a}_i-2\lambda_i{\bf a}_i =0$](img384.png)
![]() new features can be obtained by
new features can be obtained by
![\begin{displaymath}
{\bf y}_{M\times 1}={\bf A}_{M\times N}^T {\bf x}_{N\times ...
...\phi}^T_M \end{array} \right]_{M\times N} {\bf x}_{N\times 1}
\end{displaymath}](img388.png)