Next: Perceptron Learning Up: Introduction to Neural Networks Previous: Hebb's Learning
The Hopfield network
has only a single layer of ![]() nodes. It behaves as an auto-associator
(content addressable memory) with a set of
nodes. It behaves as an auto-associator
(content addressable memory) with a set of ![]() n-D vector
patterns
n-D vector
patterns
![]() stored in it. This is a
supervised method which is first trained and then used as an auto-associator.
This is a recurrent network, in the sense that the outputs of the
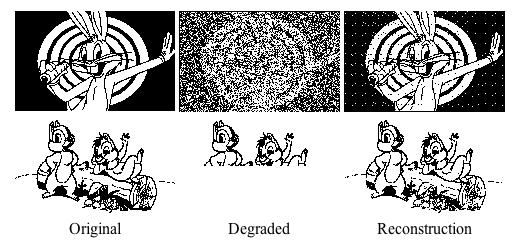
nodes are fed back in an iterative process. When an incomplete or noisy
version of one of the stored patterns is presented as the input, the
complete pattern will be generated as the output after some iterations.
stored in it. This is a
supervised method which is first trained and then used as an auto-associator.
This is a recurrent network, in the sense that the outputs of the
nodes are fed back in an iterative process. When an incomplete or noisy
version of one of the stored patterns is presented as the input, the
complete pattern will be generated as the output after some iterations.
During the classification stage after the network is trained based on the
Hebbian learning, the network can take an input pattern ![]() , a noisy
or incomplete version of one of the pre-stored pattern:
, a noisy
or incomplete version of one of the pre-stored pattern:
![$\displaystyle {\bf x}_k=[x_1^{(k)},\cdots, x_n^{(k)}]^T\;\;\;\;\;\;\;\;x_i \in\{-1,\;1\}
$](img23.svg)
![$\displaystyle {\bf y}=[y_1,\cdots, y_n]^T\;\;\;\;\;\;\;\;\;\;y_i \in\{-1,\;1\}
$](img24.svg)
Training:
The training process is essentially the same as the Hebbian learning, except
here the two associated patterns in each pair are the same (self-association),
i.e.,
![]() , and the input and output patterns all have the
same dimension
, and the input and output patterns all have the
same dimension ![]() .
.
After the network is trained by Hebbian learning its weight matrix is obtained
as the sum of the outer-products of the ![]() patterns to be stored:
patterns to be stored:
![$\displaystyle {\bf W}_{n\times n}=\frac{1}{n}\sum_{k=1}^K {\bf y}_k {\bf x}_k^T...
... \\ \vdots \\ y_n^{(k)} \end{array} \right]
[ y_1^{(k)}, \cdots, y_n^{(k)} ]
$](img25.svg)

Classification:
When the weight matrix ![]() is obtained by the training process, the
network can be used to recognize an input pattern representing some noisy
and incomplete version of one of those pre-stored patterns. When a pattern
is obtained by the training process, the
network can be used to recognize an input pattern representing some noisy
and incomplete version of one of those pre-stored patterns. When a pattern
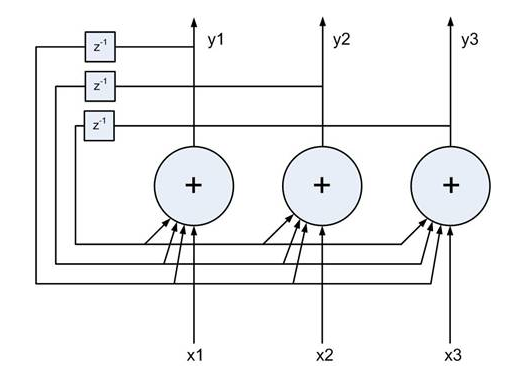
![]() is presented to the input nodes, the outputs nodes are updated
iteratively and asynchronously. Only one of the
is presented to the input nodes, the outputs nodes are updated
iteratively and asynchronously. Only one of the ![]() nodes
randomly selected is updated at a time:
nodes
randomly selected is updated at a time:

Energy function
We define the energy associated with a pair of nodes i and j as


We next define the total energy function ![]() of all
of all ![]() nodes
in the network as the sum of all pair-wise energies:
nodes
in the network as the sum of all pair-wise energies:

The iteration and convergence
Now we show that the total energy ![]() always decreases whenever
the state of any node changes. Assume
always decreases whenever
the state of any node changes. Assume ![]() has just been changeed, i.e.,
has just been changeed, i.e.,
![]() (
(![]() but
but ![]() ), while all others remain the
same
), while all others remain the
same
![]() . The energy before
. The energy before ![]() changes state is
changes state is
![$\displaystyle -\frac{1}{2}[ \sum_{i\neq k}\sum_{j\neq k}w_{ij}x_ix_j
+ \sum_i w_{ik}x_ix_k + \sum_j w_{kj}x_kx_j ]$](img122.png) |
|||
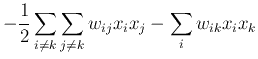 |


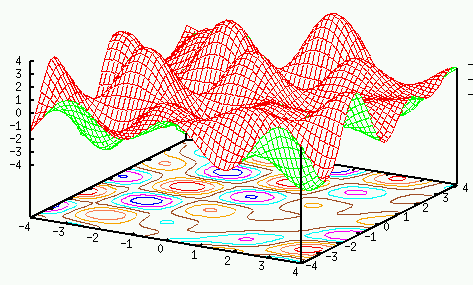
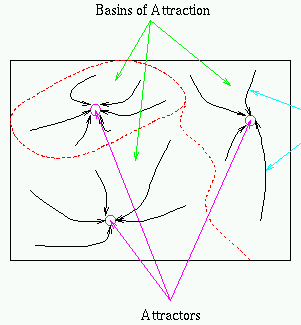
Retrieval of stored patterns
Now we show the ![]() pre-stored patterns correspond to the minima of the
energy function. First recall the weights of the network are obtained by
Hebbian learning:
pre-stored patterns correspond to the minima of the
energy function. First recall the weights of the network are obtained by
Hebbian learning:

![$\displaystyle -\frac{1}{2}\sum_{i=1}^{n} \sum_{j=1}^{n} w_{ij} x_i x_j =
-\frac...
...\frac{1}{2n}\sum_{k=1}^K \left[\sum_i \sum_j y_i^{(k)} x_i y_j^{(k)} x_j\right]$](img34.svg) |
|||
 |
Note that it is possible to have other local minima, called spurious states, which do not represent any of the stored patterns, i.e., the associative memory is not perfect.