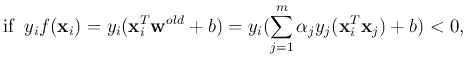This is a variation of the perceptron learning algorithm.
Consider a hyper plane in an n-dimensional (n-D) feature space:
where the weight vector 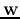 is normal to the plane, and
is normal to the plane, and 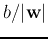 is the distance from the origin to the plane. The n-D space is partitioned
by the plane into two regions. We further define a mapping function
is the distance from the origin to the plane. The n-D space is partitioned
by the plane into two regions. We further define a mapping function
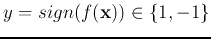 , i.e.,
Any point
, i.e.,
Any point 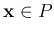 on the positive side of the plane is mapped to 1,
while any point
on the positive side of the plane is mapped to 1,
while any point 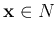 on the negative side is mapped to -1. A point
on the negative side is mapped to -1. A point
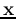 of unknown class will be classified to P if
of unknown class will be classified to P if 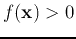 , or N
if
, or N
if 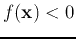 .
.
Given a set 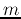 training samples from two linearly separable classes P and N:
training samples from two linearly separable classes P and N:
where
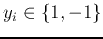 labels
labels 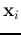 to belong to either of the two
classes. we want to find a hyper-plane in terms of
to belong to either of the two
classes. we want to find a hyper-plane in terms of 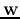 and
and 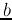 , by
which the two classes can be linearly separated.
, by
which the two classes can be linearly separated.
Before 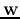 is properly trained, the actual output
is properly trained, the actual output
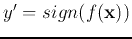 may not be the same as the desired output
may not be the same as the desired output 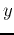 . There are four possible cases:
. There are four possible cases:
The two correct cases can also be summarized as
which is the condition a successful classifier should satisfy.
The weight vector 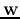 is updated whenever the result is incorrect
(mistake driven):
is updated whenever the result is incorrect
(mistake driven):
- In case 2 above,
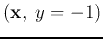 but
but 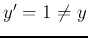 , then
When the same
, then
When the same 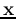 is presented again, we have
The output
is presented again, we have
The output
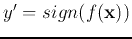 is more likely to be
is more likely to be 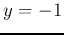 as desired.
Here
as desired.
Here 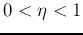 is the learning rate.
is the learning rate.
- In case 3 above,
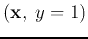 but
but 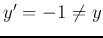 , then
When the same
, then
When the same 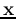 is presented again, we have
The output
is presented again, we have
The output
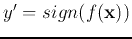 is more likely to be
is more likely to be 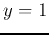 as desired.
as desired.
Summarizing the two cases, we get the learning law:
We assume initially 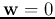 , and the
, and the 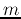 training samples are presented
repeatedly, the learning law during training will yield eventually:
training samples are presented
repeatedly, the learning law during training will yield eventually:
where 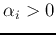 . Note that
. Note that 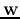 is expressed as a linear combination
of the training samples. After receiving a new sample
is expressed as a linear combination
of the training samples. After receiving a new sample
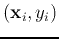 , vector
, vector
 is updated by
is updated by
Now both the decision function
and the learning law
are expressed in terms of the inner production of input vectors.


![]() training samples from two linearly separable classes P and N:
training samples from two linearly separable classes P and N:

![]() is properly trained, the actual output
is properly trained, the actual output
![]() may not be the same as the desired output
may not be the same as the desired output ![]() . There are four possible cases:
. There are four possible cases:


![]() is updated whenever the result is incorrect
(mistake driven):
is updated whenever the result is incorrect
(mistake driven):





![]() , and the
, and the ![]() training samples are presented
repeatedly, the learning law during training will yield eventually:
training samples are presented
repeatedly, the learning law during training will yield eventually: