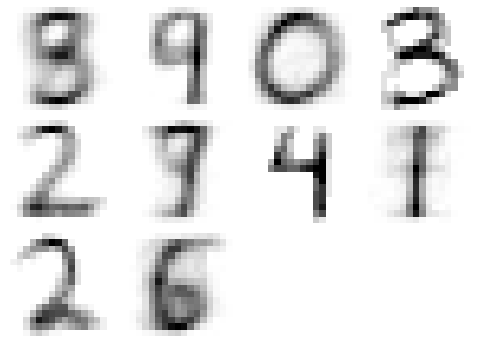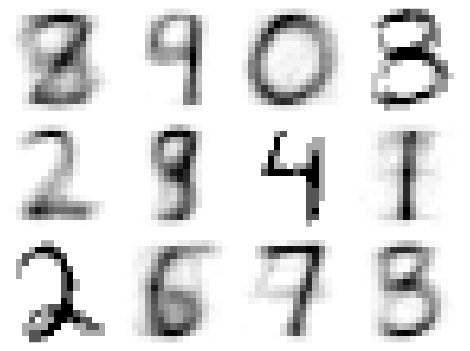If the data are binary, i.e., each data point  is treated
as a discrete random variable that takes either of two binary
values such as
is treated
as a discrete random variable that takes either of two binary
values such as  and 0 with probabilities
and 0 with probabilities  and
and  ,
then the assumption of Gaussian distribution of the dataset is
no longer valid and the Gaussian mixture model is not suitable.
In this case, the probability mass function (pmf) of the
Bernoulli distribution can be used instead:
,
then the assumption of Gaussian distribution of the dataset is
no longer valid and the Gaussian mixture model is not suitable.
In this case, the probability mass function (pmf) of the
Bernoulli distribution can be used instead:
 |
(245) |
The mean and variance of  are
are
A set of  independent binary variables can be represented
as a random vector
independent binary variables can be represented
as a random vector
![${\bf x}=[x_1,\cdots,x_d]^T$](img3.svg) with mean vector
and covariance matrix as shown below:
with mean vector
and covariance matrix as shown below:
Note that the covariance matrix
 is solely determined
by the means
is solely determined
by the means
 .
.
Now we can get the pmf of the a binary random vector  :
:
 |
(250) |
and the log pmf:
![$\displaystyle \log {\cal B}({\bf x}\vert{\bf m})
=\log\left(\prod_{i=1}^d {\cal...
...ert\mu_i)\right)
=\sum_{i=1}^d \left[ x_i\log\mu_i+(1-x_i)\log(1-\mu_i) \right]$](img905.svg) |
(251) |
Similar to the Gaussian mixture model, the Bernoulli mixture model
of  multivariate Bernoulli distributions is defined as:
multivariate Bernoulli distributions is defined as:
 |
(252) |
where
 denotes
all parameters of the mixture model to be estimated based on
the given dataset, and
denotes
all parameters of the mixture model to be estimated based on
the given dataset, and
 respect to
respect to
 . The mean of this mixture model is
. The mean of this mixture model is
 |
(253) |
Also similar to the Gaussian mixture model, we introduce a set of  latent binary random variables
latent binary random variables
![${\bf z}=[z_1,\cdots,z_K]^T$](img784.svg) with binary
conponents
with binary
conponents
 and
and
 , and get the prior
probability of
, and get the prior
probability of  , the conditional probability of
, the conditional probability of  given
given
 , and the joint probability of
, and the joint probability of  and
and  as the
following
as the
following
Given the dataset
![${\bf X}=[{\bf x}_1,\cdots,{\bf x}_N]$](img9.svg) containing
containing
 i.i.d. samples, we introduce the corresponding latent variables
in
i.i.d. samples, we introduce the corresponding latent variables
in
![${\bf Z}=[{\bf z}_1,\cdots,{\bf z}_N]$](img801.svg) , of which each
, of which each
![${\bf z}_n=[z_{n1},\cdots,z_{nK}]^T$](img802.svg) is for the labeling of
is for the labeling of  .
Then we can find the likelihood function of the Bernoulli mixture model
parameters
.
Then we can find the likelihood function of the Bernoulli mixture model
parameters
 :
:
and the log likelihood function:
Based on the same EM method used in Gaussian mixture model, we can
find the opptimal parameters that maximize the expectation of the
log likelihood function in the following two steps:
- E-step: Find the expectation of the likelihood function.
We first find the posterior probability for any sample
 to belong to cluster
to belong to cluster  , denoted by
, denoted by  :
:
which is the expectation of  :
:
 |
(260) |
Now we can find the expectation of the log likelihood with respect to
the latent variables in  :
:
- M-step: Find the optimal model parameters that maximize
the expectation of the log likelihood function.
We first set to zero the derivatives of the expectation of
the log likelihood with respect to each of the parameters in
 , and then solve
the resulting equations to get the optimal parameters.
, and then solve
the resulting equations to get the optimal parameters.
- Find
 : same as in the case of the GMM model:
: same as in the case of the GMM model:
 |
(262) |
- Find
 :
:
The ith component of the equation is
i.e.,
 |
(265) |
Solving for  we get
we get
 |
(266) |
or, in vector form,
 |
(267) |
Example:
Clustering results of hand-written digits with  and
and  . The mean
vectors
. The mean
vectors  of each of the
of each of the  clusters are visualized as shown:
clusters are visualized as shown:
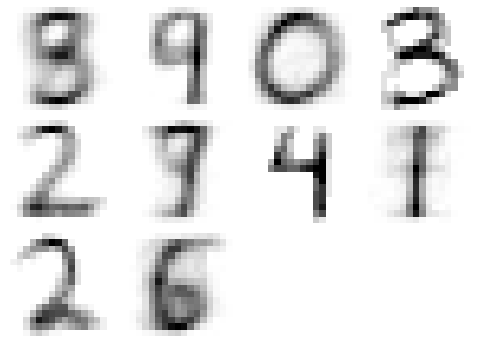
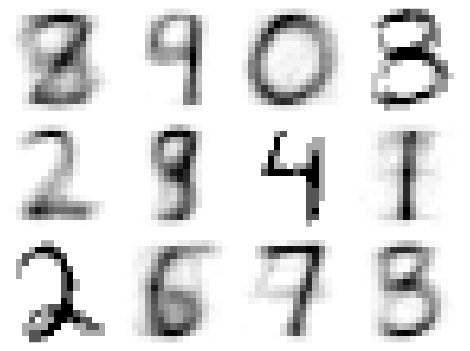





 are
are





![$\displaystyle E[(x-E(x))^2]=E(x^2)-E(x)^2$](img897.svg)


 independent binary variables can be represented
as a random vector
independent binary variables can be represented
as a random vector
![${\bf x}=[x_1,\cdots,x_d]^T$](img3.svg) with mean vector
and covariance matrix as shown below:
with mean vector
and covariance matrix as shown below:


![$\displaystyle {\bf m}=[\mu_1,\cdots,\mu_N]^T$](img900.svg)


![$\displaystyle {\bf\Sigma}=diag( \mu_i(1-\mu_i) )
=\left[ \begin{array}{ccc}
\mu_1(1-\mu_1) & & 0 \\ & \ddots & \\
0 & & \mu_d(1-\mu_d)\end{array}\right]$](img902.svg)
 is solely determined
by the means
is solely determined
by the means
 .
.


![$\displaystyle \log {\cal B}({\bf x}\vert{\bf m})
=\log\left(\prod_{i=1}^d {\cal...
...ert\mu_i)\right)
=\sum_{i=1}^d \left[ x_i\log\mu_i+(1-x_i)\log(1-\mu_i) \right]$](img905.svg)
 multivariate Bernoulli distributions is defined as:
multivariate Bernoulli distributions is defined as:

 denotes
all parameters of the mixture model to be estimated based on
the given dataset, and
denotes
all parameters of the mixture model to be estimated based on
the given dataset, and
 respect to
respect to
 . The mean of this mixture model is
. The mean of this mixture model is


![${\bf z}=[z_1,\cdots,z_K]^T$](img784.svg)
















![${\bf X}=[{\bf x}_1,\cdots,{\bf x}_N]$](img9.svg) containing
containing
 i.i.d. samples, we introduce the corresponding latent variables
in
i.i.d. samples, we introduce the corresponding latent variables
in
![${\bf Z}=[{\bf z}_1,\cdots,{\bf z}_N]$](img801.svg) , of which each
, of which each
![${\bf z}_n=[z_{n1},\cdots,z_{nK}]^T$](img802.svg) is for the labeling of
is for the labeling of  .
Then we can find the likelihood function of the Bernoulli mixture model
parameters
.
Then we can find the likelihood function of the Bernoulli mixture model
parameters
 :
:


![$\displaystyle p([{\bf x}_1,\cdots,{\bf x}_N],[{\bf z}_1,\cdots,{\bf z}_N]
\vert{\bf m}_k,P_k(k=1,\cdots,K))$](img916.svg)






![$\displaystyle \sum_{n=1}^N \sum_{k=1}^K {z_{nk}} \left[ \log P_k
+\log {\cal B}({\bf x}_n,{\bf m}_k)\right]$](img920.svg)







 :
:

 :
:


![$\displaystyle E_z\;\sum_{n=1}^N \sum_{k=1}^K z_{nk}\left[\log P_k
+\log {\cal B}({\bf x}_n,{\bf m}_k)\right]$](img926.svg)

![$\displaystyle \sum_{n=1}^N \sum_{k=1}^K E(z_{nk}) \left[\log P_k
+\log \prod_{i=1}^d \mu_{ki}^{x_{ni}} (1-\mu_{ki})^{1-x_{ni}} \right]$](img927.svg)

![$\displaystyle \sum_{n=1}^N \sum_{k=1}^K P_{nk} \left[\log P_k
+\sum_{i=1}^d \left[ x_{ni}\log\mu_{ki}+(1-x_{ni})\log(1-\mu_{ki}) \right]\right]$](img928.svg)

 : same as in the case of the GMM model:
: same as in the case of the GMM model:

 :
:


![$\displaystyle \frac{\partial}{\partial{\bf m}_k}
\sum_{n=1}^N \sum_{k=1}^K P_{n...
...sum_{i=1}^d \left[ x_{ni}\log\mu_{ki}+(1-x_{ni})\log(1-\mu_{ki}) \right]\right]$](img932.svg)

![$\displaystyle \sum_{n=1}^N P_{nk} \frac{\partial}{\partial{\bf m}_k}
\sum_{i=1}^d\left[ x_{ni}\log\mu_{ki}+(1-x_{ni})\log(1-\mu_{ki}) \right]={\bf0}$](img933.svg)
![$\displaystyle \sum_{n=1}^N P_{nk}\frac{d}{d\mu_{ki}}
\left[ x_{ni}\log \mu_{ki}+(1-x_{ni})\log(1-\mu_{ki})\right]$](img934.svg)



 we get
we get