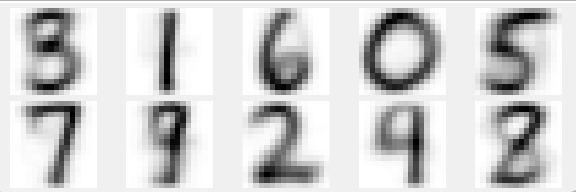K-means clustering

As suggested by the name of K-means clustering, in this method a set of $K$ mean vectors ${\bf m}_1,\cdots,{\bf m}_K$ are used to represent the clusters in the feature space, based on the assumption that there exist a set of $K$ clusters in the dataset.

The K-means clustering algorithm can be formulated as an optimization problem to minimize an objective function

$$J=\sum_{n=1}^N\sum_{k=1}^K P_{nk}\vert\vert{\bf x}_n-{\bf m}_k\vert\vert^2$$ (199)

where

$$P_{nk}=\left\{\begin{array}{ll} 1 & \mbox{if $k=\argmin_l \vert\vert{\bf x}_n-{\bf m}_l\vert\vert$}\\ 0 & \mbox{otherwise} \end{array}\right.$$ (200)

indicates that ${\bf x}_n$ is assigned to the kth cluster $C_k$ if its distance to the mean ${\bf m}_k$ is minimum. To minimize the objective function $J$ with respective to ${\bf m}_k$, we set its derivative with respect to each ${\bf m}_k$ to zero:

$$\frac{d}{d{\bf m}_k}J=2\sum_{n=1}^N P_{nk}\vert\vert{\bf x}_n-{\bf m}_k\vert\vert={\bf0} \;\;\;\;\;\;k=1,\cdots,K$$ (201)

and solve the resulting equation for ${\bf m}_k$:

$${\bf m}_k=\frac{\sum_{n=1}^N P_{nk}{\bf x}_n}{\sum_{n=1}^N P_{nk}} =\frac{1}{N_k}\sum_{{\bf x}\in C_k} {\bf x}\;\;\;\;(k=1,\cdots,K)$$ (202)

where $N_k=\sum_{n=1}^N P_{nk}$ is the number of all samples assigned to cluster $C_k$, and the summation is over all samples assigned to $C_k$.

As $P_{nk}$ depends on ${\bf m}_k$ while in turn ${\bf m}_k$ also depends on $P_{nk}$, the steps above need to be carried out iteratively, starting with $K$ randomly initialized mean vectors which are revised iteratively until convergence. Here are steps of the process:

1. Initialize randomly the mean vectors for the $K$ clusters, such as any $K$ samples of the dataset: ${\bf m}_1^{(0)},\;{\bf m}_2^{(0)},....,{\bf m}_K^{(0)}$, set iteration index to zero $l=1$;

2. Assign every sample ${\bf x}\in{\bf X}$ in the dataset to one of the $K$ clusters according to its distance to the corresponding mean vector:

   $$\;\;\; \vert\vert{\bf x}-{\bf m}_k^{(l)}\vert\vert^2 =\min_{1\le l\le K} \;\vert\vert{\bf x}-{\bf m}_l^{(l)}\vert\vert^2, \;\;\; \;\;\;\;{\bf x} \in C_k^{(l)}$$ (203)

   where $C_k^{(l)}$ denotes the kth cluster with mean vector ${\bf m}_k^{(l)}$ in the lth iteration;

3. Update the mean vectors to get the new mean ${\bf m}_k^{(l+1)}$ so that the objective function $J$ given above, i.e., the sum of the distances squared from all ${\bf x}\in C_k$ to ${\bf m}_k^{l+1}$ is minimized:

   $${\bf m}_k^{(l+1)}=\frac{1}{N_k} \sum_{{\bf x} \in C_k} {\bf x},\;\;\;\;\; (k=1,\cdots,K)$$ (204)

4. Terminate if the algorithm has converged:

   $${\bf m}_k^{(l+1)}={\bf m}_k^{(l)}\;\;\;\;(k=1,\cdots,K)$$ (205)

   Otherwise, $l \leftarrow l+1$, go back to Step 2.

This method is simple and effective, but it has the main drawback that the number of clusters $K$ needs to be estimated based on some prior knowledge, and it stays fixed through out the clustering process, even it may turn out later that the dataset may be better fit with more or fewer clusters. One way to resolve this is to carry out the algorithm multiple times with different $K$, and then evaluate each result based on the objective function $J$, or some other separability criteria, such as $tr({\bf S}_T^{-1}{\bf S}_B)$.

The Matlab code for the iteration loop of the algorithm is listed below, where Mold and Mnew are respectively the $K$ mean vectors before and after each modification. The iteration terminates when the mean vectors no longer change.

    Mnew=X(:,randi(N,1,K));          % use any K random samples as initial means
    er=inf;
    while er>0                       % main iteration
        Mold=Mnew;
        Mnew=zeros(d,K);             % initialize new means
        Number=zeros(1,K);     
        for i=1:N                    % for all N samples
            x=X(:,i);
            dmin=inf;
            for k=1:K                % for all K clusters
                d=norm(x-Mold(:,k));
                if d<dmin
                    dmin=d;  j=k;
                end
            end
            Number(j)=Number(j)+1;
            Mnew(:,j)=Mnew(:,j)+x;
        end 
        for k=1:K
            if Number(k)>0
                Mnew(:,k)=Mnew(:,k)/Number(k);
            end
        end
        er=norm(Mnew-Mold);          % terminate if means no longer change
    end

Example 1

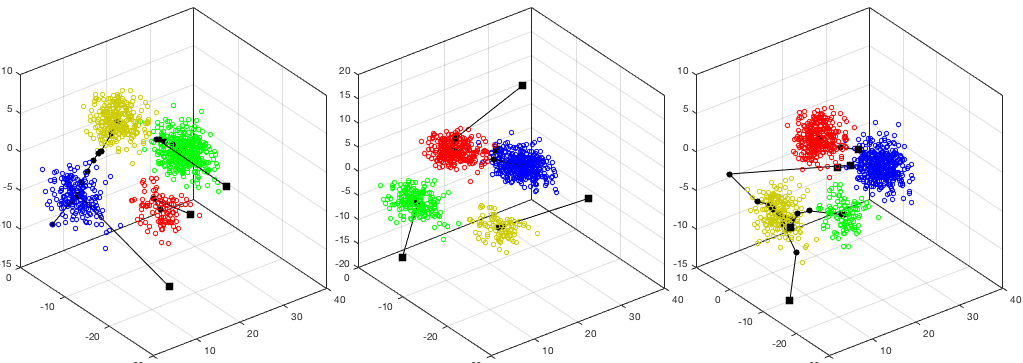
The K-means algorithm is applied to a simulated dataset in 3-D space with $C=4$ clusters. The results are shown in the figure below, where the three panels show the results corresponding to $K=C-1$ (left), $K=C$ (middle), and $K=C+1$ (right). The initial positions of the $K$ means are marked by the black squares, while their subsequent positions through out the iteration are marked by smaller dots. The iteration terminates once the means have moved to the centers of the clusters and no longer change positions.

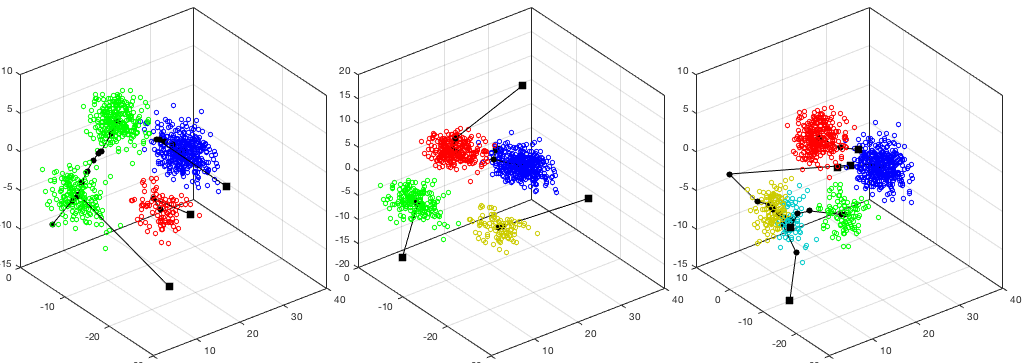
The clustering results corresponding to $K=3,\,4,\,5$ can be evaluated by the separability $tr({\bf S}_T^{-1}{\bf S}_B)$, the $K$ intra-cluster istance $tr({\bf\Sigma}_k)\,\;(k=1,\cdots,K)$ of the resulting clusters:

$$\begin{tabular}{c\vert\vert ccc\vert cccc\vert ccccc}\hline &\mul... ...1 & 44.3 & 11.8&10.8&12.7&11.1&9.1&10.8&9.1&11.1&8.9&9.4\\ \hline \end{tabular}$$ (206)

and the $K(K-1)/2$ inter-cluster (Bhattacharyya) distances (between any two of the $K$ clusters):

$$\begin{tabular}{r\vert rr}\hline \multicolumn{3}{c}{K=C-1=3} \\ \... ... 4 & 7.0 & 4.3 & 0.3 & \\ 5 &17.3 & 15.5 & 8.9 & 11.1 \\ \hline \end{tabular}$$ (207)

We see that when $K=3<C=4$, the intra-cluster distance of the 2nd cluster is significantly greater than the other two, indicating the cluster may contain two smaller clusters. Also, when $K=5>C=4$, the inter-cluster distance between clusters 3 and 4 is significantly smaller than others, indicating the two clusters are too close and can therefore be merged.

While the K-means method is simple and effective, it has the main shortcoming that the number of clusters $K$ needs to be specified, although in practice it is typically unknown a head of time. In this case, one could try different $K$ values and compare the corresponding results in terms of the intra and inter cluster distances, as well as the separabilities of the resulting clusters, as shown in the example above. Moreover, if the intra-cluster distance of a cluster is too large indicating it may contain more than one cluster (e.g., $K=3$ in the example), it can be split; on the other hand, if the inter-cluster distance between two clusters is too small (e.g., $K=5$ in the example), the two clusters may belong to the same cluster and need to be merged. Following such merging and/or splitting, a few more iterations can be carried out to make sure the final clustering results are optimal. The figure below shows the clustering results of the same dataset above but modified by merging and splliting. The left pannel is for $K=3$, but the second cluster (green) is split, while the right pannel is for $K=5$, when the 4th (yellow) and 5th (cyan) clusters are merged.

The idea of modifying the clustering results by merging and spliting leads to the algorithm of Iterative Self-Organizing Data Analysis Technique (ISODATA), which allows the number of clusters $K$ to be adjusted automatically during the iteration by merging clusters close to each other and splitting clusters with large intra-cluster distances. However, this algorithm is highly heuristic as the various parameters such the threshold values for merging and splitting need to be specified.

Example 2

The K-means clustering method is applied to the dataset of ten handwritten digits from 0 to 9 used previously. The clustering result is visualized based on the KLT that maps the data samples in the original 256-D space into the 3-D space spanned by the three eigenvectors corresponding to the three greatest eigenvalues of the covariance matrix of the dataset. The ground truth labelings are color coded as shown on the left, while the clustering result is shown on the right. We see that the clustering results match the original data reasonably well.

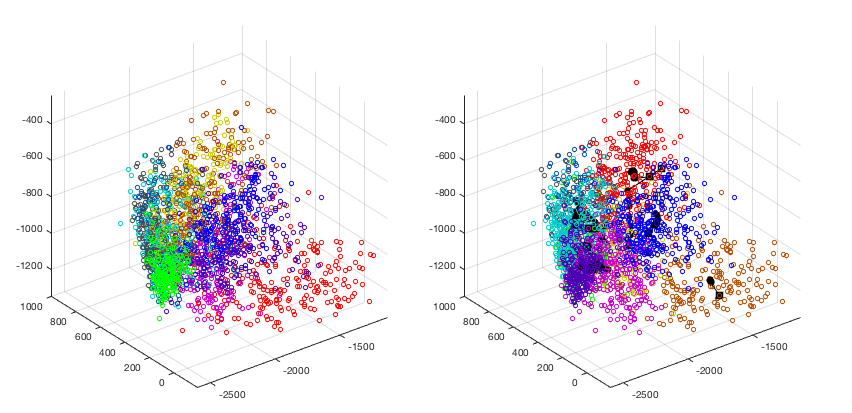
The clustering result is also shown in the confusion matrix, of which the columns and rows represent respectively the clusters based on the K-means clustering and the ground truth labeling (not used). In other words, the element in the ith row and jth column is the number of samples labeled to belong to the ith class but assigned to the jth cluster.

$$\left[ \begin{array}{rrrrrrrrrr} 1 & 0 & 25 & 165 & 27 & 2 & 3 & ... ...2 & 0 & 54 \\ 4 & 2 & 0 & 1 & 0 & 28 & 119 & 1 & 64 & 5 \\ \end{array}\right]$$ (208)

All samples are converted from 256-dimensional vector back to $16\times 16$ image form and the averages of the samples in each of the ten cluster are shown in the figure below. We see that each of the ten clusters clearly represents one distinct digit.