Discriminative vs. Generative Methods for Classification

As one of the most important tasks in machine learning, pattern classification is to classify some objects of interest, generically referred to as patterns and described by a set of $d$ features or attributes that characterizes the patterns, to one of some $K$ classes or categories. Each pattern is represented by a vector (or a point) ${\bf x}=[x_1,\cdots,x_d]^T$ in a d-dimensional feature space, where $x_i\;(i=1,\cdots,d)$ is a variable for the measurement of the ith feature. Symbolically, the $K$ classes can be denoted $\{C_1,\cdots,C_K\}$, and a pattern ${\bf x}$ belonging to the kth class is denoted by ${\bf x}\in C_k$. Pattern classification can therefore be considered as the process by which the d-dimensional feature space is partitioned into $K$ regions each corresponding to one of the $K$ classes. The boundaries between these regions, called decision boundaries, are to be determined by the specific algorithm, called a classifier, used for the classification.

Pattern classification can be carried out as either a supervised or unsupervised learning process, depending on the availability of a training set containing patterns of known class identities. Specifically, the training set contains a set of $N$ patterns in ${\bf X}=[{\bf x}_1,\cdots,{\bf x}_N]$, labeled respectively by the corresponding component in ${\bf y}=[ y_1,\cdots,y_N]^T$ representing the class identities of the corresponding patterns in some way. For example, we can use $y_k \in \{1,\cdots,K\}$ to indicate ${\bf x}_k \in C_{y_k}$. In the special case when $K=2$, there are only two classes $C_1=C_+$ and $C_0=C_-$, and the classifier becomes binary based on training pattern ${\bf x}_j\;(j=1,\cdots,N)$, each labeled by $y_j=1$ if ${\bf x}_j\in C+$ or $y_j=-1$ if ${\bf x}_j\in C_-$.

We assume there are $N_k$ training samples $\{{\bf x}_1^{(k)},\cdots,{\bf x}_{N_k}^{(k)}\}$ all labeled to belong to $C_k,\;\;(k=1,\cdots,K)$, and in total $N=\sum_{k=1}^K N_k$ samples in the training set. If the training set is a fair representation of all patterns of different classes in the entire dataset, then $P_k=N_k/N$ can be treated as an estimate of the a priori probability that any randomly selected pattern ${\bf x}$ happens to belong to class $C_k$, without any prior knowledge of the pattern.

Once a classifier is properly trained according to a specific algorithm based on the traning set, the feature space is partitioned into regions corresponding to the different classes and any unlabeled pattern of unknown class as a vector ${\bf x}$ in the feature space can be classified into one of the $K$ classes.

Supervised classification can be considered as a process of establishing the corresponding relationship between the patterns ${\bf x}_1,\cdots, {\bf x}_N$ treated as the independent or input variables to the classifier, and the classes $C_1,\cdots,C_K$ the input patterns belong, treated as the dependent or output variables. Therefore regression and classification can be considered as the same supervised learning process: modeling the relationship between the data points in $\{ {\bf x}_1,\cdots,{\bf x}_N\}$ and their corresponding labelings (or targets) in $\{ y_1,\cdots,y_N\}$. This process is regression when the labelings take continous real values, but it is classification when they are discrete categorical representing different classes. Some methods in the previous chapter on regression analysis are actually used as classifiers, such as logistic and solfmax regressions, and the method of Gaussian process can also be used for classification.

If the training data of labeled patterns are unavailable, various unsupervised learning methods can be used to assign each unlabeled patterns into one of the $K$ different groups, called clusters, according to its position in the feature space, based on the overall spatial structure and distribution of the data set in the feature space. This process is called clustering analysis or simply clustering.

There exsit a variety of methods for learning, including both regression and classification, based on different models assumed. One way to characterize these methods is to put them all in a probabilistic framework, in terms of the probabilities of the given dataset incuding data points ${\bf X}$ and the corresponding labeling ${\bf y}$. Now a method can be categorized into either of the following two groups:

• Discriminative model (conditional or backward model)

  A discriminative method stablishes a model that maps a data pont ${\bf x}$ to a class labeling $y$. Such a model is either a pure or traditional discriminative model if it is deterministic and aims to fit the training set in some optimal way, or a conditional model if it is probabilistic in nature, such as the conditional probability $p(y\vert{\bf x})$. The model parameters in ${\bf\theta}$ are obtained in some optimal way based on the training set. Then prediction can be made for any unlabeled ${\bf x}$ in terms of the corresponding $y$. As a discriminative method aims at finding the decision boundaries between different classes based on the training set, only those data samples that are close to the boundaries play an important role, while all other samples farther away from the boundaries are mostly ignored.

  Typical discrimiative methods include:

  • K-nearest neighbors algorithm
  • Linear and logistic regressions
  • Support vector machines
  • Perceptrons and Neural networks
  • Decision trees and random forests

• Generative model (forward model)

  A generative method first assumes certain probabilistic model for the underlying structure of the observed data, such the joint probability $p({\bf x},y\vert{\bf\theta})$ based on all data samples available. It then estimates the parameter ${\bf\theta}$ of the model based on the training dataset, and obtains the conditional probability $p(y\vert{\bf x})$ (by Bayes' theorem) based on which a prediction can be made for any unlabeled ${\bf x}$ to find the corresponding $y$. As in general the generative method is based on some probabilistic model of the data, it can be used for unsupervised learning as well as supervised.

  Typical generative methods include:

  • Naive Bayes classifiers
  • Gaussian mixture classifiers
  • Hidden Markov model

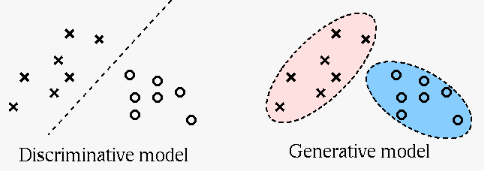
Here are some comparisons between the two approaches:

• The discriminative methods find the decision boundary in the feature space directly based on the data points in the training set, in general they
  • are simpler than the generative approach requiring problem-specific knowledge for building models of the data,
  • are effective in producing accurate result when the dataset is large
  • provide no insight or interpretation regarding the data and no uncertainty estimate

• The generative methods first establish a probabilistic model for the underlying structure of the data as an effort to explain how the data was generated, and then finds the decision boundary based the model. In general, they
  • allow the use of problem-specific knowlege for building the model,
  • can provide explanation and interpretation of the data,
  • may be less prone to overfitting than a discriminative method,
  • can provide uncertainty estimate
  • may not be as accurate as the discriminative methods if the model does not fit the dataset well.