The mutual information  of two random variables
of two random variables  and
and  is
defined as
is
defined as
 |
(216) |
Obviously when  and
and  are independnent, i.e.,
are independnent, i.e.,
 and
and
 , their mutual information
, their mutual information  is zero.
is zero.
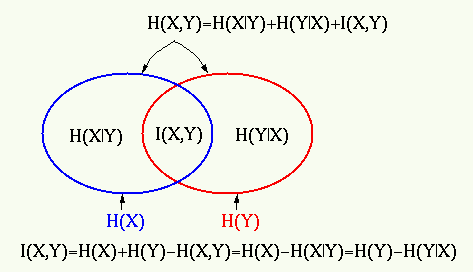
Similarly the mutual information
 of a set of
of a set of  variables
variables  (
(
 ) is defined as
) is defined as
 |
(217) |
If random vector
![${\bf y}=[y_1,\cdots,y_n]^T$](img810.svg) is a linear transform of
another random vector
is a linear transform of
another random vector
![${\bf x}=[x_1,\cdots,x_n]^T$](img811.svg) :
:
 or or |
(218) |
then the entropy of  is related to that of
is related to that of  by:
by:
where
 is the Jacobian of the above transformation:
is the Jacobian of the above transformation:
 |
(220) |
The mutual information above can be written as
We further assume  to be uncorrelated and of unit variance, i.e., the
covariance matrix of
to be uncorrelated and of unit variance, i.e., the
covariance matrix of  is
is
 |
(222) |
and its determinant is
 |
(223) |
This means
 is a constant (same for any
is a constant (same for any  ). Also,
as the second term in the mutual information expression
). Also,
as the second term in the mutual information expression
 is also a constant (invariant with respect to
is also a constant (invariant with respect to  ), we have
), we have
 Constant Constant |
(224) |
i.e., minimization of mutual information
 is achieved
by minimizing the entropies
is achieved
by minimizing the entropies
 |
(225) |
As Gaussian density has maximal entropy, minimizing entropy is equivalent
to minimizing Gaussianity.
Moreover, since all  have the same unit variance, their negentropy
becomes
have the same unit variance, their negentropy
becomes
 |
(226) |
where  is the entropy of a Gaussian with unit variance, same
for all
is the entropy of a Gaussian with unit variance, same
for all  . Substituting
. Substituting
 into the expression of
mutual information, and realizing the other two terms
into the expression of
mutual information, and realizing the other two terms
 and
and
 are both constant (same for any
are both constant (same for any  ), we get
), we get
 |
(227) |
where  is a constant (including all terms
is a constant (including all terms  ,
,
 and
and
 ) which is the same for any linear transform matrix
) which is the same for any linear transform matrix
 . This is the fundamental relation between mutual information and
negentropy of the variables
. This is the fundamental relation between mutual information and
negentropy of the variables  . If the mutual information of a set
of variables is decreased (indicating the variables are less dependent)
then the negentropy will be increased, and
. If the mutual information of a set
of variables is decreased (indicating the variables are less dependent)
then the negentropy will be increased, and  are less Gaussian. We
want to find a linear transform matrix
are less Gaussian. We
want to find a linear transform matrix  to minimize mutual information
to minimize mutual information
 , or, equivalently, to maximize negentropy (under the
assumption that
, or, equivalently, to maximize negentropy (under the
assumption that  are uncorrelated).
are uncorrelated).




 and
and  are independnent, i.e.,
are independnent, i.e.,
 and
and
 , their mutual information
, their mutual information  is zero.
is zero.
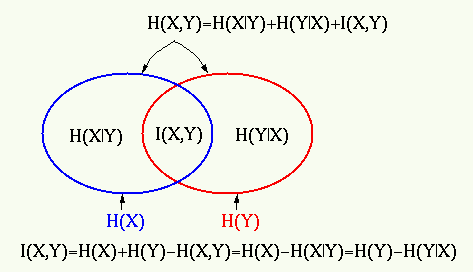





![${\bf y}=[y_1,\cdots,y_n]^T$](img810.svg) is a linear transform of
another random vector
is a linear transform of
another random vector
![${\bf x}=[x_1,\cdots,x_n]^T$](img811.svg) :
:
 or
or
 is related to that of
is related to that of  by:
by:





 is the Jacobian of the above transformation:
is the Jacobian of the above transformation:






 to be uncorrelated and of unit variance, i.e., the
covariance matrix of
to be uncorrelated and of unit variance, i.e., the
covariance matrix of  is
is


 is a constant (same for any
is a constant (same for any  ). Also,
as the second term in the mutual information expression
). Also,
as the second term in the mutual information expression
 is also a constant (invariant with respect to
is also a constant (invariant with respect to  ), we have
), we have
 Constant
Constant is achieved
by minimizing the entropies
is achieved
by minimizing the entropies



 is the entropy of a Gaussian with unit variance, same
for all
is the entropy of a Gaussian with unit variance, same
for all  . Substituting
. Substituting
 into the expression of
mutual information, and realizing the other two terms
into the expression of
mutual information, and realizing the other two terms
 and
and
 are both constant (same for any
are both constant (same for any  ), we get
), we get

 is a constant (including all terms
is a constant (including all terms  ,
,
 and
and
 ) which is the same for any linear transform matrix
) which is the same for any linear transform matrix
 . This is the fundamental relation between mutual information and
negentropy of the variables
. This is the fundamental relation between mutual information and
negentropy of the variables  . If the mutual information of a set
of variables is decreased (indicating the variables are less dependent)
then the negentropy will be increased, and
. If the mutual information of a set
of variables is decreased (indicating the variables are less dependent)
then the negentropy will be increased, and  are less Gaussian. We
want to find a linear transform matrix
are less Gaussian. We
want to find a linear transform matrix  to minimize mutual information
to minimize mutual information
 , or, equivalently, to maximize negentropy (under the
assumption that
, or, equivalently, to maximize negentropy (under the
assumption that  are uncorrelated).
are uncorrelated).