Next: Minimization of Mutual Information Up: Methods of ICA Estimations Previous: Non-Gaussianity is Independence
The ICA method depends on certain measurement of the non-Gaussianity:
Kurtosis is defined as the normalized form of the fourth central moment of a distribution:
 |
(209) |
 to have zero mean
to have zero mean
 and unit variance
and unit variance
 , then
, then
 and
and
 .
Kurtosis measures the degree of peakedness (spikiness) of a distribution
and it is zero only for Gaussian distribution. Any other distribution's
kurtosis is either positive if it is supergaussian (spikier than Gaussian)
or negative if it is subgaussian (flatter than Gaussian). Therefore the
absolute value of the kurtosis or kurtosis squared can be used to measure
the non-Gaussianity of a distribution. However, kurtosis is very sensitive
to outliers, and it is not a robust measurement of non-Gaussianity.
.
Kurtosis measures the degree of peakedness (spikiness) of a distribution
and it is zero only for Gaussian distribution. Any other distribution's
kurtosis is either positive if it is supergaussian (spikier than Gaussian)
or negative if it is subgaussian (flatter than Gaussian). Therefore the
absolute value of the kurtosis or kurtosis squared can be used to measure
the non-Gaussianity of a distribution. However, kurtosis is very sensitive
to outliers, and it is not a robust measurement of non-Gaussianity.
The entropy of a random variable 

 |
(210) |
 .
(And uniform distribution has the maximum entropy among all distributions
over a finite range.) Based on this property, the differential entropy,
also called negentropy, is defined as
.
(And uniform distribution has the maximum entropy among all distributions
over a finite range.) Based on this property, the differential entropy,
also called negentropy, is defined as
 |
(211) |
 is a Gaussian variable with the same variance as
is a Gaussian variable with the same variance as  .
As
.
As  is always greater than zero unless
is always greater than zero unless  is Gaussian, it is
a good measurement of non-Gaussianity.
is Gaussian, it is
a good measurement of non-Gaussianity.
This result can be generalized from random variables to random vectors,
such as
![${\bf y}=[y_1,\cdots,y_m]^T$](img143.svg)






The negentropy can be approximated by
 |
(212) |
![$\displaystyle J(y)\approx \sum_{i=1}^p k_i [ E\{G_i(y)\}-E\{G_i(g)\}]^2$](img796.svg) |
(213) |
 are some positive constants,
are some positive constants,  is assumed to have zero mean
and unit variance, and
is assumed to have zero mean
and unit variance, and  is a Gaussian variable also with zero mean and
unit variance.
is a Gaussian variable also with zero mean and
unit variance.  are some non-quadratic functions such as
are some non-quadratic functions such as
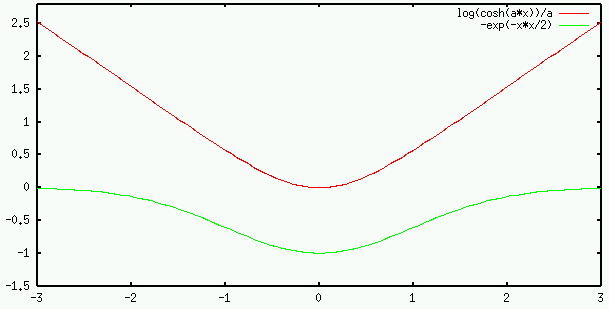
 |
(214) |
 is some suitable constant. Although this approximation
may not be accurate, it is always greater than zero except when
is some suitable constant. Although this approximation
may not be accurate, it is always greater than zero except when  is
Gaussian. In particular, when
is
Gaussian. In particular, when  , we have
, we have
![$\displaystyle J(y)=[E\{ G(y)\}-E\{G(g)\}]^2$](img801.svg) |
(215) |
 to
maximize
to
maximize  .
.