t-Distributed Stochastic Neighbor Embedding (t-SNE)

It is impossible to reduce the dimensionality of a given dataset which is intrinsically high-dimensional (high-D), while still preserving all the pairwise distances in the resulting low-dimensional (low-D) space, compromise will have to be made to sacrifice certain aspects of the dataset when the dimensionality is reduced.

The PCA method as a linear, dimensionality reduction algorithm,

is unable to interpret complex nonlinear relationship between features. tance preserving method, the PCA emphasizes the importance of the PCA dimensions with great variances, but neglects small distance variations. It places distant and dissimilar data points far apart in the low-D space, while ignoring the importance of similar datapoints close together in the high-D, which need to be also placed close together in the low-D space. Therefore the PCA method tends to preserve large scale global structure of the dataset, while ignoring the small scale local structure.

But in some cases the local structures are of equal or even more importance than the global ones, such as the typical example of “Swiss roll”.

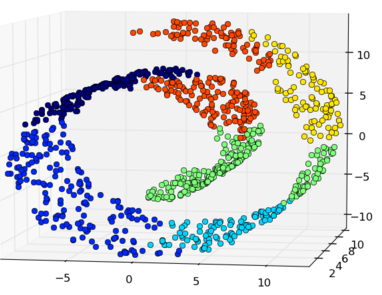
Also, when the dimensionality is much reduced from a high-D space to a low-D space, the crowding problem occurs. In a high-D space, a data point may have a large number of similar neighbors of roughly equal distance; however, in a low-D space, the number of equal-distance neighbors is significantly reduced (8 in a 3-D space, 4 in a 2-D space, 2 in a 1-D space). Thus the space available for the neighbors of a point is much reduced. As the result, when a large number of neighbors in the high-D are mapped to a low-D space, they are forced to spread out, some are getting closer to those that are farther away in the original space, thereby reducing the gaps between potential clusters of similar points.

In contrast, the t-SNE method is a nonlinear method that is based on probability distributions of the data points being neighbors, and it attempts to preserve the structure at all scales, but emphasizing more on the small scale structures, by mapping nearby points in high-D space to nearby points in low-D space.

The similarity between any two distinct points ${\bf x}_i$ and ${\bf x}_j$ in the high-D space is defined as a probability based on the Gaussian kernel:

$$p_{ij}= \frac{\exp(-\vert\vert{\bf x}_i-{\bf x}_j\vert\vert^2/2\s... ...f x}_l\vert\vert^2/2\sigma^2)}, \;\;\;\;\;\;\;\;\;\;\;\; \sum_i\sum_j p_{i/j}=1$$ (185)

However, if ${\bf x}_i={\bf x}_j$, $p_{ij}=0$ is defined to be zero, as it never needed in the algorithm. Note that $p_{ij}$ is a probability measurement as it is normalized and add up to 1.

If ${\bf x}_j$ is close to ${\bf x}_j$, $\vert\vert{\bf x}_i-{\bf x}_j\vert\vert$ is small and $p_{ij}$ is large, indicating ${\bf x}_j$ is similar to ${\bf x}_i$; but if ${\bf x}_j$ is far away from ${\bf x}_j$, $\vert\vert{\bf x}_i-{\bf x}_j\vert\vert$ is large and $p_{ij}$ is small, indicating ${\bf x}_j$ is dissimilar to ${\bf x}_i$. Also, as $\sum_i\sum_j p_{ij}=1$, $p_{ij}$ can be considered as a probability that any two points ${\bf x}_j$ and ${\bf x}_i$ are neighbors in the feature space and are therefore similar to each other.

Similarly, we could also define the similarity $q_{ij}$ in the low-D space also based on the Gaussian kernel. However, for reason explained below, we prefer to define the similarity $q_{in}$ in the low-D space based on Student's t-distribution of degree 1, instead of Gaussian distribution:

$$q_{ij}=\frac{(1+\vert\vert{\bf y}_i-{\bf y}_j\vert\vert^2)^{-1}} {\sum_k\sum_{l\ne k}(1+\vert\vert{\bf y}_k-{\bf y}_l\vert\vert^2)^{-1}}$$ (186)

As shown in the figure below, when compared with the Gaussian distribution, the t-distribution has a lower peak in the center but higher tails on the sides. It is because of this property, the t-distribution is used to address the crowding problem. Let ${\bf x}_i$ be the point of interest (black, in the center of the Gaussian kernel), then another point ${\bf x}_j$ (red) is mapped to a different position, which is closer to ${\bf x}_i$ if they are initially close (similar), or farther away from each other if they are initially far apart (dissimilar).

How well the points ${\bf y}_i$ in the low-D space represent the similarity relationship among the points ${\bf x}_i$ in the original high-D space can be measured by the discrepancy bwtween the two sets of probabilities, measured by the cost function, defined as the Kullback-Leibler divergence:

$$C=KL(P\vert\vert Q)=\sum_i\sum_j p_{ij} \log\frac{p_{ij}}{q_{ij}} =\sum_i\sum_j \left( p_{ij} \log p_{ij} - p_{ij} \log q_{ij}\right)$$ (187)

We desire to find the optimal map points ${\bf y}_i$ in the low-D space that minimize the discrepancy $C=KL(P\vert\vert Q)$.

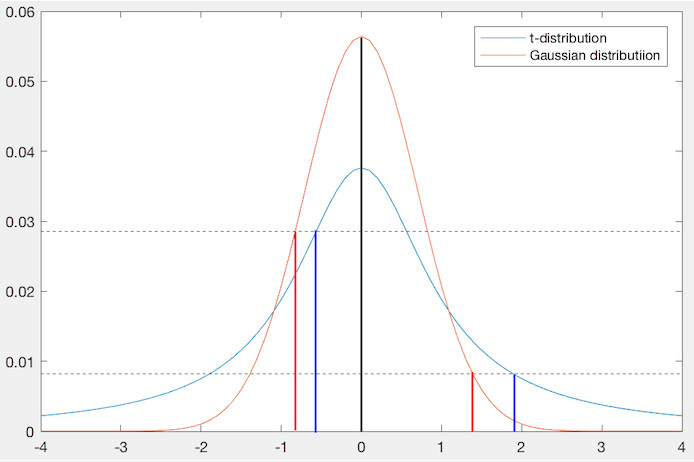
The KL divergence is not symmetric as $KL(P\vert\vert Q)\ne KL(Q\vert\vert P)$, therefore it can not be viewed as a distance between the two sets of probabilities. This asymmetry is actually a desired feature. Consider the following two cases:

• If $p_{ij}$ is large but $q_{ij}$ is small, the cost $C$ is very large, i.e., and such a mapping is heavily penalized. As the result, similar points that are close to each other in the high-D space tend to be mapped to points in the low-D space that are also close to each other.

• If $p_{ij}$ is small but $q_{ij}$ is large, the cost $C$ is small, i.e., such a mapping is not heavily penalized. As the result, dissimilar points that are far apart in the high-D space are allowed to be mapped to points in the low-D space that are closer to each other.

We therefore see that minimizing the KL divergence has the effect of preserving the local structure of the dataset, but not necessarily the global structure.

Before proceeding to consider the minimization of the cost function $C$, we still need to resolve two additional issues:

• One potential problem with $p_{ij}$ defined above is that when a point ${\bf x}_i$ is an outlier with large distances $\vert\vert{\bf x}_i-{\bf x}_j\vert\vert$ to every other point ${\bf x}_j$ in the dataset, $p_{ij}$ is small and insignificant in the cost function $C$, and the location of ${\bf y}_i$ in the low-D space can not be well determined. To resolve this issue, we redefine $p_{ij}$ as the average of two conditioinal probablities:

  $$p_{ij}=\frac{p_{i/j}+p_{j/i}}{2n}$$ (188)

  where $n$ is the total number of data points and

  $$p_{i/j}=\frac{\exp(-\vert\vert{\bf x}_i-{\bf x}_j\vert\vert^2/2\s... ...rt{\bf x}_i-{\bf x}_k\vert\vert^2/2\sigma^2_i)}, \;\;\;\;\;\;\;\sum_i p_{j/i}=1$$ (189)

  is the conditional probability that any point ${\bf x}_j$ is a neighboring point similar to a given point ${\bf x}_i$. Note that $p_{j/i}$ is properly normalized and add up to 1:

  $$\sum_{j=1}^n \sum_{i=1}^n p_{i/j} =\frac{1}{2n}\sum_{i=1}^n \left... ...ht) =\frac{1}{2n}\sum_{i=1}^n 1 +\frac{1}{2n}\sum_{j=1}^n 1=\frac{1}{2n}(n+n)=1$$ (190)

  i.e., it is a probability measurement.

• Whether two points are close (therefore similar) to each other needs to be measured relatively, independent of the local data density, which may vary in different local regions of the feature space. We can therefore use different variance $\sigma_i$ for $p_{j/i}$ depending on the local data density in the neighborhood of ${\bf x}_i$. Specifically, we choose $\sigma_i$ in such a way that the perplexity $2^{H(p_i)}$ is the same for all data points, i.e., the entropy $H(p_i)=-\sum_j p_{j/i}\log_2 p_{j/i}$ representing the uncertainty is the same, independent of the local data density. As shown here, the entropy of a Gaussian $p(x,\mu,\sigma)$ is $\log(2\pi e \sigma^2)/2$, a monotonic function of its variance $\sigma$.

We can now find the optimal map points ${\bf y}_i$ that minimize the cost function $C=KL(P\vert\vert Q)$, by gradient descent method.

To find the gradient of $\partial C/\partial{\bf y}_i$, we first introduce a set of intermediate variables

$$d_{kl}=\vert\vert{\bf y}_k-{\bf y}_l\vert\vert =\left[({\bf y}_k-... ...;\;\;\;\;(k,l=1,\cdots,n),\;\;\;\;\;\;\; Z=\sum_k\sum_{l\ne k}(1+d_{kl}^2)^{-1}$$ (191)

so that

$$q_{ij}=\frac{(1+\vert\vert{\bf y}_i-{\bf y}_j\vert\vert^2)^{-1}} ... ...ij}^2)^{-1}}{\sum_k\sum_{l\ne k}(1+d_{kl}^2)^{-1}} =\frac{(1+d_{ij}^2)^{-1}}{Z}$$ (192)

Note that

$$\frac{\partial Z}{\partial d_{ij}} =\frac{\partial}{\partial d_{ij}} \left[\sum_k\sum_{l\ne k}(1+d_{kl}^2)^{-1}\right] =-2d_{ij}(1+d_{ij}^2)^{-2}$$ (193)

We now find $\partial C/\partial{\bf y}_i$ based on chain-rule. Note that when ${\bf y}_i$ changes, only $d_{ij}$ and $d_{ji}$ (for all $j$) change, we therefore have

$$\frac{\partial C}{\partial {\bf y}_i} =\sum_j \frac{\partial C}{\... ..._j \frac{\partial C}{\partial d_{ji}}\frac{\partial d_{ji}}{\partial {\bf y}_i}$$ (194)

But as

$$\frac{\partial d_{ij}}{\partial{\bf y}_i} =\frac{\partial d_{ji}}... ...f y}_j)\right]^{-1/2}2({\bf y}_i-{\bf y}_j) =\frac{{\bf y}_i-{\bf y}_j}{d_{ij}}$$ (195)

we have

$$\frac{\partial C}{\partial {\bf y}_i} =\sum_j\left( \frac{\partia... ...} =2\sum_j \frac{\partial C}{\partial d_{ij}}\frac{{\bf y}_i-{\bf y}_j}{d_{ij}}$$ (196)

We next find $\partial C/\partial d_{ij}$. Note that only $q_{kl}$ may be a function of $d_{ij}$, while all $p_{kl}$ are constants, we therefore have

$$\frac{\partial C}{\partial d_{ij}} = \frac{\partial}{\partial d_{ij}} \left[\sum_k\sum_{l\ne k} \left(... ...right] =-\sum_k\sum_{l\ne k} p_{kl} \frac{\partial}{\partial d_{ij}}\log q_{kl}$$

$$= -\sum_k\sum_{l\ne k} p_{kl} \frac{\partial}{\partial d_{ij}} (\lo... ...d_{ij}} (1+d_{kl}^2)^{-1} +\frac{1}{Z}\frac{\partial Z}{\partial d_{ij}}\right)$$

$$= p_{ij} \left(\frac{1}{q_{ij}Z} (1+d_{ij}^2)^{-2}\,2d_{ij} \right) -\left(\sum_k\sum_{l\ne k} p_{kl}\right)\;\frac{1}{Z}(1+d_{ij}^2)^{-2}\,2d_{ij}$$

$$= 2d_{ij}\left[\frac{p_{ij}}{q_{ij}} \frac{(1+d_{ij}^2)^{-2}}{Z}-\frac{(1+d_{ij}^2)^{-2}}{Z}\right]$$ (197)

The second to the last equality is due to $\partial (1+d_{kl}^2)^{-1}/\partial d_{ij}=0$ when $i\ne k$ or $j\ne l$, and the last equality is due to $\sum_k\sum_{l\ne k} p_{kl}=1$. But as

$$\frac{(1+d_{ij}^2)^{-2}}{Z}=q_{ij}(1+d_{ij}^2)^{-1}$$ (198)

The above becomes

$$\frac{\partial C}{\partial d_{ij}} =2d_{ij}\left(\frac{p_{ij}}{q_... ...}-1\right) \frac{(1+d_{ij}^2)^{-2}}{Z} =2d_{ij}(p_{ij}-q_{ij})(1+d_{ij}^2)^{-1}$$ (199)

We can now finally get the gradient vector of the cost function $C$ with respect to each of the map points ${\bf y}_i$:

$$\frac{\partial C}{\partial {\bf y}_i} = 2\sum_j \frac{\partial C}{\partial d_{ij}}\frac{{\bf y}_i-{\bf y}_j}{d_{ij}} =4(p_{ij}-q_{ij})(1+d_{ij}^2)^{-1}({\bf y}_i-{\bf y}_j)$$

$$= 4\sum_j (p_{ij}-q_{ij})\left( 1+\vert\vert{\bf y}_i-{\bf y}_j\vert\vert^2\right)^{-1} ({\bf y}_i-{\bf y}_j)$$ (200)

Given the gradient vector, we can iteratively approach the optimal data points in the low-D space that minimize the discrepancy $C=KL(P\vert\vert Q)$:

$${\bf y}_{n+1}={\bf y}_n+\delta \frac{\partial C}{\delta{\bf y}} +\alpha_n({\bf y}_n-{\bf y}_{n-1})$$ (201)

where $\delta$ is the step size (learning rate) and the second term is momentum term.