2-D Interpolation

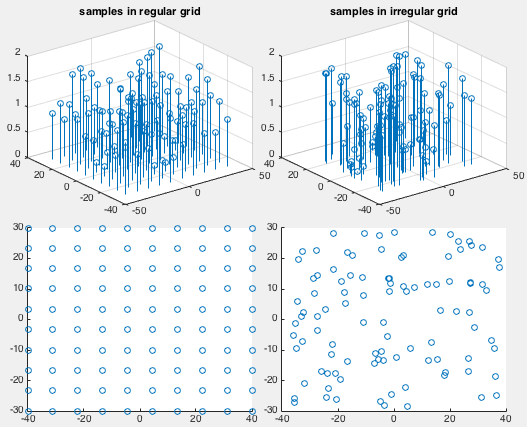
Interpolation can also be carried out in 2-D space. Given a set of sample points $v({\bf x}_i)=f(x_i,\,y_i),\,(i=1,\cdots,n)$ at 2-D points ${\bf x}_i=[x_i,y_i]^T$ in either a regular grid or an irregular grid (scattered data points), we can construct an interpolating function $f({\bf x})=f(x,y)$ that passes through all these sample points. Here we will first consider methods based only on regular grids and then those that also work for irregular grids.

Methods based on sample points in regular grid

• Bilinear Interpolation

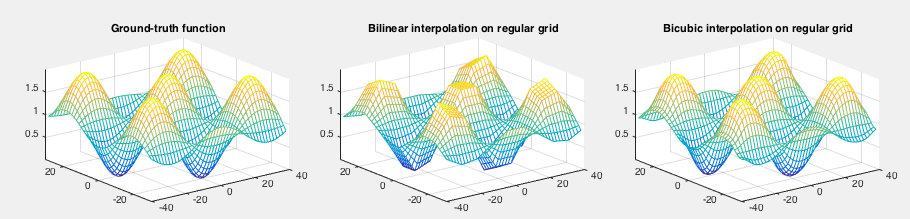
  Given a set of 2-D sample points in a regular grid, we can use the methods of bilinear and bicubic 2-D interpolation to obtain the value of the interpolating function $f(x,y)$ at any point $(x,y)$ inside each of the rectangles in a 2-D grid with the four corners at $(x_i,\,y_j)$, $(x_{i+1},\,y_{j+1})$, $(x_i,\,y_{j+1})$, and $(x_{i+1},\,y_{j+1})$. In the following, for convenience and without loss of generality, we only consider one of such rectangles with $i=j=0$, and define $\delta x=x-x_0$, $\delta y=y-y_0$, $\Delta x=x_1-x_0$, and $\Delta y=y_1-y_0$.

  First recall that $f(x)$ at any point $x$ in the 1-D interval $x_0<x<x_1$ can be approximated by linear interpolation based on $f_0=f(x_0)$ and $f_1=f(x_1)$:

  $$\frac{f(x)-f_0}{f_1-f_0}=\frac{x-x_0}{x_1-x_0}=\frac{\delta x}{\Delta x}, \;\;\;\;\; \;\;\;\;\; f(x)=\frac{\delta x}{\Delta x}(f_1-f_0)+f_0 \\$$

  

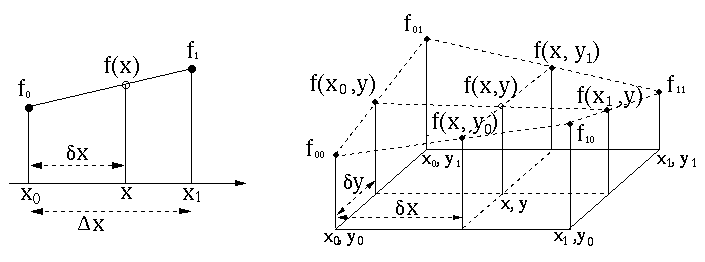
  This method of 1-D linear interpolation can be extended to the bilinear interpolation method to calculate the function value $f(x,y)$ at any 2-D point with $x_0<x<x_1$ and $y_0<x<y_1$ based on the known sample values $f_{00}=f(x_0,y_0)$, $f_{01}=f(x_0,y_1)$, $f_{10}=f(x_1,y_0)$, and $f_{11}=f(x_1,y_1)$ at the four corners of the rectangle in a 2-D grid. This is carried out in the following two steps:

  • Linear interpolation in x-dimension:
    

    $$f(x,y_0) = \frac{\delta x}{\Delta x}(f_{10}-f_{00})+f_{00}$$

    $$f(x,y_1) = \frac{\delta x}{\Delta x}(f_{11}-f_{01})+f_{01}$$

    
    
  • Linear interpolation in y-dimension:
    

    $$f(x,y) = \frac{dy}{\Delta y}[f(x,y_1)-f(x,y_0)]+f(x,y_0)$$

    $$= \frac{dy}{\Delta y} \left[\frac{\delta x}{\Delta x}(f_{11}-f_{01}... ...}(f_{10}-f_{00})-f_{00}\right] +\frac{\delta x}{\Delta x}(f_{10}-f_{00})+f_{00}$$

    $$= \frac{\delta x}{\Delta x}\frac{dy}{\Delta y}f_{11} +\frac{dy}{\De... ...{dy}{\Delta y} +\frac{\delta x}{\Delta x}\frac{\delta y}{\Delta y}\right)f_{00}$$ (98)

    
    

  As the final expression for the bilinear interpolation is symmetric with respect to $x$ and $y$, the order of the two steps is irrelevant, i.e., if the interpolation is first carried out in y-direction and then in x-direction, the result is exactly the same.

• Bicubic Interpolation

  The same set of 2-D sample points can be more smoothly approximated by a bicubic function in the following form:

  $$f(x,y)\approx C(x,y)=\sum_{i=0}^3\sum_{j=0}^3a_{ij}x^iy^j \\$$

  where the 16 weights $a_{ij}\;(i,j=0,\cdots,3)$ can be found by assuming that at the four corners $(0,0)$, $(1,0)$, $(0,1)$ and $(1,1)$ of the rectangle in which $(x,y)$ resides, $C(x,y)$ and $f(x,y)$ have the same partial derivative values as well as function values:

  $$\left\{ \begin{array}{lll} f_{00}=f(0,0)&=&C(0,0)=a_{00}\\ f... ...y}(1,1)=\sum_{i=0}^3\sum_{j=0}^3ija_{ij} \end{array}\right. \\$$

  These 16 equations can be expressed in matrix form as:

  $${\bf A}{\bf a}= \left[\begin{array}{cccccccccccccccc} 1 & 0 & 0 &... ...}(0,0)\\ f_{xy}(1,0)\\ f_{xy}(0,1)\\ f_{xy}(1,1)\end{array}\right] ={\bf f} \\$$

  Solving this linear system of 16 equations, we get the 16 weights in the bicubic model of the function:

  $${\bf a}={\bf A}^{-1}{\bf f}= \left[\begin{array}{c}a_{00}\\ a_{10... ...\\ f_{xy}(0,0)\\ f_{xy}(1,0)\\ f_{xy}(0,1)\\ f_{xy}(1,1)\end{array}\right] \\$$

  

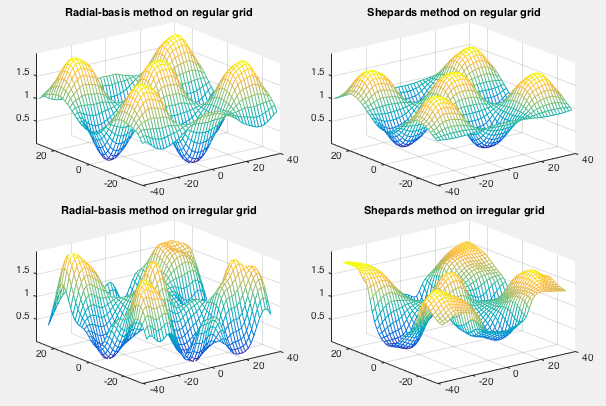
Methods based on sample points in irregular grid

The methods discussed above require the data points to be available on a regular (rectangular) grid. They do not work if the data points are hileramdomly scattered in the 2-D space (irregular grid). We now discuss methods that work for both regular and irregular grids.

• Radial Basis Function Method

  A radial basis function (RBF) is any function that is centrally symmetric with respect to a specific point ${\bf x}_0=[x_0, y_0]^T$, i.e., the value of the RBF at any 2-D point ${\bf x}=[x,\,y]^T$ can be simply represented by $\phi_0({\bf x})=\phi(\vert\vert{\bf x}-{\bf x}_0\vert\vert)$, as a function of the distance $d({\bf x},{\bf x}_0)=\vert\vert{\bf x}-{\bf x}_0\vert\vert=\sqrt{(x-x_0)^2+(y-y_0)^2}$ between the point and ${\bf x}_0$. Typical RBFs include the Gaussian and Butterworth functions:

  $$\phi_c({\bf x})=exp\left(-\frac{ \vert\vert{\bf x}-{\bf x}_0\vert... ..._c({\bf x})=\frac{1}{1+(\vert\vert{\bf x}-{\bf x}_0\vert\vert/\sigma)^{2k}} \\$$

  where $\sigma$ is a parameter that controls the width of the RBF. By adjusting $\sigma$ we can achieve the desired smoothness of the interpolating function based on the density of the scatter data points (average distance between any two points). The parameter $k$ in the Butterworth function is the order of the function which controls the shape of the function

  

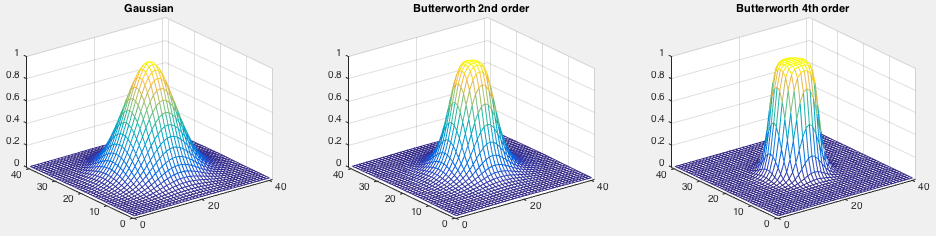
  Based on a given RBF $\phi({\bf x})$, we can construct an interpolating function $f(x,y)=f({\bf x})$ as the weighted sum of such RBFs each centered around one of the given sample points $v({\bf x}_i),\;(i=1,\cdots,n)$:

  $$f({\bf x})=\sum_{i=1}^n w_i\, \phi_i({\bf x})=\sum_{i=1}^n w_i\, \phi(\vert\vert{\bf x}-{\bf x}_i\vert\vert) \\$$

  Here the weights $w_i$ are determined based on the requirement that the interpolating function takes the same value as the sample point at each of the $n$ positions:

  $$f({\bf x}_j)=\sum_{i=1}^n w_i \phi(\vert\vert{\bf x}_i-{\bf x}_j\vert\vert) =v({\bf x}_j),\;\;\;\;\;\;(j=1,\cdots,n) \\$$

  Solving this equation system of $n$ linear equations with $n^2$ coefficients $\phi(\vert\vert{\bf x}_i-{\bf x}_j\vert\vert)$, we get the weights $w_1,\cdots,w_n$ and thereby the interpolation function $f({\bf x})$.

• Shepards method

  In this method, the value of the interpolating function $f({\bf x})$ at any 2-D point ${\bf x}=(x,y)$ is calculated as the weighted average of all available sample points:

  $$f({\bf x})=\sum_{i=1}^n w_i({\bf x})\, v({\bf x}_i) \\$$

  where $w_i({\bf x})$ is the weight function that is inversely proportional the pth power of the distance $d({\bf x},{\bf x}_i)=\vert\vert{\bf x}-{\bf x}_i\vert\vert$ between ${\bf x}$ and ${\bf x}_i$, and normalized:

  $$w'_i({\bf x})=\frac{1}{d({\bf x},{\bf x}_i)^p},\;\;\;\;\;\;\; w_i({\bf x})=\frac{w'_i({\bf x})}{\sum_{k=1}^n w'_k({\bf x})} \\$$

  so that $\sum_{i=1}^nw_i({\bf x})=1$. Here the parameter $p>1$ controls the rate of decay of $w'_i({\bf x})=1/d({\bf x},{\bf x}_i)^p$ as the distance $d({\bf x},{\bf x}_i)$ becomes greater. Similar to the parameter $\sigma$ in the RBF method, here $p$ can also be adjusted according the density of the sample points to control the smoothness of the interpolating function $f({\bf x})$.

  In particular, at any sample point ${\bf x}={\bf x}_j$, we have

  $$d({\bf x},{\bf x}_i)=d({\bf x}_j,{\bf x}_i) \left\{\begin{array}{... ...\left\{\begin{array}{ll}=\infty & i=j\\ <\infty & i\ne j \end{array}\right. \\$$

  and

  $$w_i({\bf x})=w_i({\bf x}_j)=\frac{w'_i({\bf x}_j)}{\sum_{k=1}^n w... ...\delta_{ij}=\left\{\begin{array}{ll}1 & i=j\\ 0 & i\ne j\end{array}\right., \\$$

  we therefore get

  $$f({\bf x}_j)=\sum_{i=1}^n w_i({\bf x}_j)\, v({\bf x}_i) =\sum_{i=1}^n \delta_{ij}v({\bf x}_i)=v({\bf x}_j) \\$$

  i.e., the interpolating function is guaranteed to go through every sample point. Note that in code realization, care needs to be taken to aviod the issue of “devide by zero”.

  The weight function $w'_i({\bf x})=1/d({\bf x},{\bf x}_i)$ can be generalized to any RBF function centrally symmetric with respect to ${\bf x}_i$, such as the Gaussian or Butterworth fucntions considered above:

  $$w'_i({\bf x})=exp\left(-\frac{ \vert\vert{\bf x}-{\bf x}_i\vert\v... ... w'_i({\bf x})=\frac{1}{1+(\vert\vert{\bf x}-{\bf x}_i\vert\vert/\sigma)^2} \\$$

  which can then be normalized as before. Here we also need to guarantee that the resulting interpolating function passes all given sample points, i.e., $f({\bf x}_i)=v({\bf x}_i)$ for all $i=1,\cdots,n$. To do so, we can set $w'_i({\bf x})=\infty$ (a very large number in practicd) when ${\bf x}={\bf x}_i$, so that $w_i({\bf x}_j)=\delta_{ij}$. and $f({\bf x}_i)=v({\bf x}_i)$ for all $i=1,\cdots,n$.