It is often needed to estimate the value of a function  at
certan point
at
certan point  based on the known values of the function
based on the known values of the function
 at a set of
at a set of  node points
node points
 in the interval
in the interval ![$[a,\; b]$](img16.svg) . This process is called
interpolation if
. This process is called
interpolation if  or extrapolation if either
or extrapolation if either
 or
or  . One way to carry out these operations is to
approximate the function
. One way to carry out these operations is to
approximate the function  by an nth degree polynomial:
by an nth degree polynomial:
 |
(1) |
where the  coefficients
coefficients
 can be obtained based
on the
can be obtained based
on the  given points. Once
given points. Once  is available, any operation
applied to
is available, any operation
applied to  , such as differentiation, intergration, and root
finding, can be carried out approximately based on
, such as differentiation, intergration, and root
finding, can be carried out approximately based on
 .
This is particulary useful if
.
This is particulary useful if  is non-elementary and therefore
difficult to manipulate, or it is only available as a set of discrete
samples without a closed-form expression.
is non-elementary and therefore
difficult to manipulate, or it is only available as a set of discrete
samples without a closed-form expression.
Specifically, to find the coefficients of  , we require it
to pass through all node points
, we require it
to pass through all node points
 ,
i.e., the following
,
i.e., the following  linear equations hold:
linear equations hold:
 |
(2) |
Now the coefficients
 can be found by solving these
can be found by solving these
 linear equations, which can be expressed in matrix form as:
linear equations, which can be expressed in matrix form as:
![$\displaystyle \left[ \begin{array}{ccccc}
1 & x_0 & x_0^2 & \cdots & x_0^n \\
...
...\left[\begin{array}{c}y_0\\ y_1\\ y_2\\ \vdots\\ y_n\end{array}\right]
={\bf y}$](img27.svg) |
(3) |
where
![${\bf a}=[a_0,\cdots,a_n]^T$](img28.svg) ,
,
![${\bf y}=[y_0,\cdots,y_n]^T$](img29.svg) ,
and
,
and
![$\displaystyle {\bf V}=\left[ \begin{array}{ccccc}
1 & x_0 & x_0^2 & \cdots & x_...
...vdots & \ddots & \vdots \\
1 & x_n & x_n^2 & \cdots & x_n^n
\end{array}\right]$](img30.svg) |
(4) |
is known as the Vandermonde matrix. Solving this linear
equation system, we get the coefficients
![$[a_0,\cdots,a_n]^T={\bf a}={\bf V}^{-1}{\bf y}$](img31.svg) .
Here
.
Here  polynomials
polynomials
 can be considered
as a set of polynomial basis functions that span the space of all
nth degree polynomials (which can also be spanned by any other
possible bases).
If the node points
can be considered
as a set of polynomial basis functions that span the space of all
nth degree polynomials (which can also be spanned by any other
possible bases).
If the node points
 are distinct, i.e.,
are distinct, i.e.,  has a full rank and its inverse
has a full rank and its inverse
 exists, then the
solution of the system
exists, then the
solution of the system
 is unique and
so is
is unique and
so is  .
.
In practice, however, this method is not widely used for two
reasons: (1) the high computational complexity  for
calculating
for
calculating
 , and (2) matrix
, and (2) matrix  becomes
more ill-conditioned as
becomes
more ill-conditioned as  increases. Instead, other methods
to be discussed in the following section are practically used.
increases. Instead, other methods
to be discussed in the following section are practically used.
The error of the polynomial interpolation is defined as
 |
(5) |
which is non-zero in general, except if  at which
at which
 . In other words, the error function
. In other words, the error function
 has
has  zeros at
zeros at
 , and can therefore be
written as
, and can therefore be
written as
 |
(6) |
where  is an unknown function and
is an unknown function and  is a polynomial
of degree
is a polynomial
of degree  defined as
defined as
 |
(7) |
To find  , we construct another function
, we construct another function  of variable
of variable  with any
with any
 as a parameter:
as a parameter:
 |
(8) |
which is zero when  :
:
 |
(9) |
We therefore see that  has
has  zeros at
zeros at
 and
and
 . According to Rolle's theorem, which states that the derivative
function
. According to Rolle's theorem, which states that the derivative
function  of any differentiable function
of any differentiable function  satisfying
satisfying
 must have at least a zero at some point
must have at least a zero at some point
 at which
at which  ,
,  has at least
has at least  zeros each between
two consecutive zeros of
zeros each between
two consecutive zeros of  ,
,  has at least
has at least  zeros,
and
zeros,
and
 has at least one zero at some
has at least one zero at some
 :
:
The last equation is due to the fact that  and
and
 are respectively an nth and (n+1)th degree polynomials of
are respectively an nth and (n+1)th degree polynomials of  . Solving the
above we get
. Solving the
above we get
 |
(11) |
Now the error function can be written as
 |
(12) |
where  is a point located anywhere between
is a point located anywhere between  and
and
 dependending on
dependending on  . The error can be quantitatively
measured by the 2-normal of
. The error can be quantitatively
measured by the 2-normal of  :
:
 |
(13) |
In particular, if  is a polynomial of degree
is a polynomial of degree  , then
, then
 , and it can be exactly interpolated by
, and it can be exactly interpolated by  . But
if
. But
if  , the interpolation has a non-zero error term
, the interpolation has a non-zero error term  . In
particular, if
. In
particular, if  is a polynomial of degree
is a polynomial of degree  , such as
, such as
 , then
, then
 and the error term becomes:
and the error term becomes:
 |
(14) |
Due to the uniqueness of the polynomial interpolation, the error
analysis above also applies to all other methods to be considered in
the following sections, such as the Lagrange and Newton interpolations.
Example:
Approximate function
 by a polynomial
by a polynomial
 of degree
of degree  , based on the following
, based on the following  node points:
node points:
We first find the Vandermonde matrix:
and get the coefficients:
and then the interpolating polynomial can be found as a weighted sum
of the first  power functions used as the basis functions to
span the polynomial space:
This interpolation polynomial
power functions used as the basis functions to
span the polynomial space:
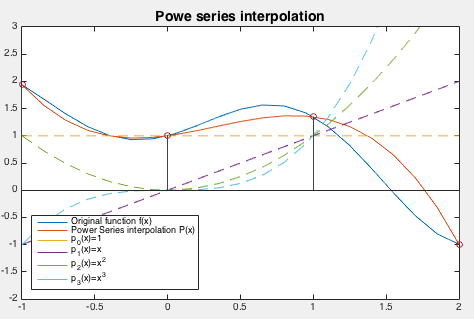
This interpolation polynomial  is plotted in the figure below,
in comparison to the orginal function
is plotted in the figure below,
in comparison to the orginal function  , together with the basis
polynomials, the power functions
, together with the basis
polynomials, the power functions
 . The error
. The error
 can be approximated by a set of
can be approximated by a set of  discrete samples
discrete samples
 of the function
of the function  and the interpolating polynomial
and the interpolating polynomial
 :
:
The Matlab code that implements this method is listed below.
function [v P]=PI(u,x,y)
% vectors x and y contain n+1 points and the corresponding function values
% vector u contains all discrete samples of the continuous argument of f(x)
n=length(x); % number of interpolating points
k=length(u); % number of discrete sample points
v=zeros(1,k); % polynomial interpolation
P=zeros(n,k); % power function basis polynomials
V=zeros(n); % Vandermonde matrix
for i=1:n
for j=1:n
V(i,j)=x(i)^(j-1);
end
end
c=inv(V)*y; % coefficients
for i=1:n
P(i,:)=u.^(i-1);
v=v+c(i)*P(i,:);
end
end





![$[a,\; b]$](img16.svg)





 coefficients
coefficients
 can be obtained based
on the
can be obtained based
on the  given points. Once
given points. Once  is available, any operation
applied to
is available, any operation
applied to  , such as differentiation, intergration, and root
finding, can be carried out approximately based on
, such as differentiation, intergration, and root
finding, can be carried out approximately based on
 .
This is particulary useful if
.
This is particulary useful if  is non-elementary and therefore
difficult to manipulate, or it is only available as a set of discrete
samples without a closed-form expression.
is non-elementary and therefore
difficult to manipulate, or it is only available as a set of discrete
samples without a closed-form expression.




 can be found by solving these
can be found by solving these
 linear equations, which can be expressed in matrix form as:
linear equations, which can be expressed in matrix form as:
![$\displaystyle \left[ \begin{array}{ccccc}
1 & x_0 & x_0^2 & \cdots & x_0^n \\
...
...\left[\begin{array}{c}y_0\\ y_1\\ y_2\\ \vdots\\ y_n\end{array}\right]
={\bf y}$](img27.svg)
![${\bf a}=[a_0,\cdots,a_n]^T$](img28.svg) ,
,
![${\bf y}=[y_0,\cdots,y_n]^T$](img29.svg) ,
and
,
and
![$\displaystyle {\bf V}=\left[ \begin{array}{ccccc}
1 & x_0 & x_0^2 & \cdots & x_...
...vdots & \ddots & \vdots \\
1 & x_n & x_n^2 & \cdots & x_n^n
\end{array}\right]$](img30.svg)
![$[a_0,\cdots,a_n]^T={\bf a}={\bf V}^{-1}{\bf y}$](img31.svg) .
Here
.
Here  polynomials
polynomials
 can be considered
as a set of polynomial basis functions that span the space of all
nth degree polynomials (which can also be spanned by any other
possible bases).
If the node points
can be considered
as a set of polynomial basis functions that span the space of all
nth degree polynomials (which can also be spanned by any other
possible bases).
If the node points
 are distinct, i.e.,
are distinct, i.e.,  has a full rank and its inverse
has a full rank and its inverse
 exists, then the
solution of the system
exists, then the
solution of the system
 is unique and
so is
is unique and
so is  .
.





 at which
at which
 . In other words, the error function
. In other words, the error function
 has
has  zeros at
zeros at
 , and can therefore be
written as
, and can therefore be
written as

 is an unknown function and
is an unknown function and  is a polynomial
of degree
is a polynomial
of degree  defined as
To find
defined as
To find  , we construct another function
, we construct another function  of variable
of variable  with any
with any
 as a parameter:
as a parameter:

 :
:

 has
has  zeros at
zeros at
 and
and
 . According to Rolle's theorem, which states that the derivative
function
. According to Rolle's theorem, which states that the derivative
function  of any differentiable function
of any differentiable function  satisfying
satisfying
 must have at least a zero at some point
must have at least a zero at some point
 at which
at which  ,
,  has at least
has at least  zeros each between
two consecutive zeros of
zeros each between
two consecutive zeros of  ,
,  has at least
has at least  zeros,
and
zeros,
and
 has at least one zero at some
has at least one zero at some
 :
:


![$\displaystyle \frac{d^{n+1}}{dt^{n+1}}
\left[ f(t)-P_n(t)-u(x)\prod_{i=0}^n(t-x_i) \right]_{t=\xi}$](img64.svg)

![$\displaystyle \left[f^{(n+1)}(t)+P_n^{(n+1)}(t)-u(x)\frac{d^{n+1}}{dt^{n+1}}\prod_{i=0}^n(t-x_i)\right]_{t=\xi}$](img65.svg)


 and
and
 are respectively an nth and (n+1)th degree polynomials of
are respectively an nth and (n+1)th degree polynomials of  . Solving the
above we get
. Solving the
above we get

 is a point located anywhere between
is a point located anywhere between  and
and
 dependending on
dependending on  . The error can be quantitatively
measured by the 2-normal of
. The error can be quantitatively
measured by the 2-normal of  :
:

















![$\displaystyle {\bf V}=\left[ \begin{array}{cccc}
1 & x_0 & x_0^2 & x_0^3 \\
1 ...
...-1 \\
1 & 0 & 0 & 0 \\
1 & 1 & 1 & 1 \\
1 & 2 & 4 & 9 \end{array}\right]
\\ $](img86.svg)
![$\displaystyle {\bf a}={\bf V}^{-1}{\bf y}={\bf V}^{-1}
\left[\begin{array}{r}f(...
...ht]
=\left[\begin{array}{r}1.000\\ 0.369\\ 0.643\\ -0.663\end{array}\right]
\\ $](img87.svg)
 power functions used as the basis functions to
span the polynomial space:
power functions used as the basis functions to
span the polynomial space:

 is plotted in the figure below,
in comparison to the orginal function
is plotted in the figure below,
in comparison to the orginal function  , together with the basis
polynomials, the power functions
, together with the basis
polynomials, the power functions
 . The error
. The error
 can be approximated by a set of
can be approximated by a set of  discrete samples
discrete samples
 of the function
of the function  and the interpolating polynomial
and the interpolating polynomial
 :
:
![$\displaystyle \epsilon=\vert\vert R_3(x)\vert\vert _2=\left(\int_a^b R^2_3(x)\,...
...prox \left(\frac{1}{k}\sum_{i=1}^k [f(u_i)-P_3(u_i)]^2 \right)^{1/2}=0.3063
\\ $](img93.svg)
