Linear Programming (LP)

The basic problem in linear programming (LP) is to minimize/maximize a linear objective function $f(x_1,\cdots,x_N)=\sum_{i=1}^N c_ix_i$ of $N$ variables $x_1,\cdots,x_N$ under a set of $M$ linear constraints:

$$\begin{tabular}{ll} max: & $f(x_1,\cdots,x_N)=\sum_{i=1}^N c_ix_i... ..._{Mi}x_i \le b_M\\ x_1\ge 0,\cdots,x_N\ge 0 \end{array} \right.$ \end{tabular}$$ (209)

The LP problem can be more concisely represented in matrix form:

$$\begin{tabular}{ll} max: & ${\bf c}^T{\bf x}$\ \\ s. t.: & $\lef... ... Ax}-{\bf b}\le {\bf0}\\ {\bf x}\ge {\bf0}\end{array}\right.$\\ \end{tabular}$$ (210)

where

$${\bf x}=\left[\begin{array}{c}x_1\\ \vdots\\ x_N\end{array}\right... ...ts&a_{1N}\\ \vdots & \ddots & \vdots \\ a_{M1}&\cdots&a_{MN}\end{array}\right]$$ (211)

and the smaller or greater than sign in a vector inequality should be understood as an element-wise relationship between the corresponding elements of the vectors on both sides.

For example, the objective function could be the total profit, the constraints could be some limited resources. Spicifically, $x_1,\cdots,x_N$ may represent the quantities of $N$ different types of products, $c_1,\cdots,c_N$ represent their unit prices, and $a_{ij}$ represent the consumption of the ith resource by the jth product, the goal is to maximize the profit $f(x_1,\cdots,x_N)$ subject to the constraints imposed by the limited resources $b_1,\cdots,b_M$.

Here all variables are assumed to be non-negative. If there exists a variable that is not restricted, it can be eliminated. Specifically, we can solve one of the constraining equations for the variable and use the resulting expression of the variable to replace all its appearances in the problem. For example:

$$\begin{tabular}{ll} max: & $f(x_1,x_2,x_3)=2x_1-x_2+3x_3$\ \\ s.... ...1-x_2+4x_3=10 \\ x_2 \ge 0,\;\; x_3\ge 0 \end{array} \right.$\\ \end{tabular}$$ (212)

Solving the first constraining equation for the free variable $x_1$, we get $x_1=3+2x_2-x_3$. Substituting this into the objective function and the other constraint, we get $2x_1-x_2+x_3=3x_2+x_3+6$ and $5x_2+x_3=1$, the problem can be reformulated as:

$$\begin{tabular}{ll} max: & $f(x_2,x_3)=3x_2+x_3+6$\ \\ s. t.: & ... ...}{l} 5x_2+x_3=1 \\ x_2 \ge 0,\;\; x_3\ge 0\end{array}\right.$\\ \end{tabular}$$ (213)

Given the primal LP problem above, we can further find its dual problem. We first construct the Lagrangian of primal problem:

$$L({\bf x})={\bf c}^T{\bf x}-{\bf y}^T({\bf Ax}-{\bf b}) =({\bf c}-{\bf A}^T{\bf y})^T{\bf x}+{\bf y}^T{\bf b}$$ (214)

where ${\bf y}=[y_1,\cdots,y_M]^T$ contains the Lagrange multipliers for the inequality constraints ${\bf Ax}-{\bf b}\le{\bf0}$, and ${\bf y}\ge{\bf0}$ according to Table 188. We define the dual function as the maximum of $L({\bf x})$ over ${\bf x}$:

$$f_d({\bf y})=\max_{\bf x} L({\bf x}) =\max_{\bf x} [ {\bf c}^T{\b... ...bf b}) ] =\max_{\bf x} [ ({\bf c}-{\bf A}^T{\bf y})^T{\bf x}+{\bf y}^T{\bf b} ]$$ (215)

To find the value of ${\bf x}$ that maximizes $L({\bf x})$, we set its gradient to zero and get:

$$\bigtriangledown_{\bf x}L({\bf x}) =\bigtriangledown_{\bf x}[ ({\... ...}-{\bf A}^T{\bf y})^T{\bf x}+{\bf y}^T{\bf b}] ={\bf c}-{\bf A}^T{\bf y}={\bf0}$$ (216)

Substituting this into $L_d({\bf y})=\max_{\bf x}L({\bf x})$ we get: $f_d({\bf y})={\bf y}^T{\bf b}$, which is the upper bound of $f_p({\bf x})$, under the constraint that ${\bf c}-{\bf A}^T{\bf y}\le 0$ so that $({\bf c}-{\bf A}^T{\bf y})^T{\bf x}\le 0$ contributes negatively to $L({\bf x})$ (as ${\bf x}\ge 0$):

$$f_d({\bf y})={\bf b}^T{\bf y}\ge L({\bf x}) ={\bf c}^T{\bf x}-{\bf y}^T({\bf Ax}-{\bf b}) \ge{\bf c}^T{\bf x}=f_p({\bf x})$$ (217)

This upper bound needs to be minimized with respect to ${\bf y}$, to become the tightest upper bound, i.e., the original primal problem of maximization in Eq. (210) has now been converted into the following dual problem of minimization:

$$\left\{\begin{array}{ll}\mbox{max}: & {\bf c}^T{\bf x}\\ \mbox{s... ...t.} & {\bf A}^T{\bf y}-{\bf c}\ge{\bf0},\;\; {\bf y}\ge{\bf0}\end{array}\right.$$ (218)

Following the same approach, we can also find the dual of a minimization primal problem:

$$\left\{\begin{array}{ll}\mbox{min}: & {\bf c}^T{\bf x}\\ \mbox{s... ...t.} & {\bf A}^T{\bf y}+{\bf c}\ge{\bf0},\;\; {\bf y}\ge{\bf0}\end{array}\right.$$ (219)

Moreover, we can show that the dual of a dual problem is the original primal problem.

If either the primal or the dual is feasible and bounded, so is the other, and they form a strong duality, the solution $d^*$ of the dual problem is the same as the solution $p^*$ of the primal problem. Also, as the primal and dual problems are completely symmetric.

An inequality constrained LP problem can be converted to an equality constrained problem by introducing slack variables:

$$\sum_{i=1}^N a_ix_i\le b \;\;\;\Longrightarrow\;\;\; \sum_{i=1}^N a_ix_i + s = b,\;\;\;(s\ge 0)$$ (220)

so that it can be reformulated to take the standard form:

$$\begin{tabular}{ll} max: & $z=f({\bf x})={\bf c}^T{\bf x}=\sum_{j... ...\cdots,& x_N\ge 0, &s_1\ge 0,&\cdots& s_M\ge 0\end{array}\right.$ \end{tabular}$$ (221)

We further redefine the following:

• ${\bf x}$ is an $N+M$ dimensional augmented variable vector that includes the $M$ slack variables $\{s_1,\cdots,s_M\}$ as well as the $N$ original variables $\{x_1,\cdots,x_N\}$:

  $${\bf x}=[x_1,\;x_2,\cdots,x_N,\,s_1,\;s_2,\cdots,s_M]^T$$ (222)

• ${\bf A}$ is redefined as an $M\times (N+M)$ augmented coefficient matrix that includes coefficients for both types of variables:

  $${\bf A}=\left[\begin{array}{cccc\vert cccc} a_{11} & a_{12} & \cd... ...\right]_{M\times (N+M)} =[\;{\bf A}_{M\times N}\;\vert\; {\bf I}_{M\times M}\;]$$ (223)

  where ${\bf A}_{M\times N}$ are the coefficients for the $N$ original variables $\{x_1,\cdots,x_N\}$, and the identity matrix ${\bf I}_{M\times M}=[{\bf e}_1,\cdots,{\bf e}_M]$ is for the unity coefficients of the $M$ slack variables $\{s_1,\cdots,s_M\}$, each of which appears in the $M$ constraints only once.

Now the LP problem can be expressed in the standard form (original form on the left, with ${\bf x}$ and ${\bf A}$ redefined on the right):

$$\begin{tabular}{ll} max: & ${\bf c}^T{\bf x}$\\ s. t.: & $\left\... ...}\ge{\bf0},\;{\bf s}\ge{\bf0} \end{array}\right.$ \end{tabular}\;\;\;\;\;\;\;\; \;\;\;\;\;\; \begin{tabular}{ll} max: & ${\bf c}^T{\bf x}$\\ s. ... ...{l} {\bf A}{\bf x}={\bf b}\\ {\bf x}\ge{\bf0} \end{array}\right.$ \end{tabular}$$ (224)

An LP problem can be viewed geometrically. If normalize ${\bf c}$ so that $\vert\vert{\bf c}\vert\vert=1$, then the objective function $f({\bf x})={\bf c}^T{\bf x}$ becomes the projection of ${\bf x}$ onto ${\bf c}$. Each of the $M$ equality constraints in ${\bf A}{\bf x}={\bf b}$ represents a hyper-plane in the N-D vector space perpendicular to its normal direction ${\bf a}_j=[a_{i1},\cdots,a_{IN}]^T$:

$$\sum_{j=1}^N a_{ij}x_j={\bf a}_j^T{\bf x}=b_i,\;\;\;\;\;\;\;(i=1,\cdots,M)$$ (225)

Also, each of the $N$ non-negativity conditions $x_j\ge 0$ in ${\bf x}\ge{\bf0}$ corresponds to a hyper-plane perpendicular to the jth standard basis vector ${\bf e}_j$. In general, in an N-D space, if none of the hyper-planes is parallel to any others, then no more than $N$ hyper-planes intersect at one point. For example, in a 2-D or 3-D space, two straignt lines or three surfaces intersect at a point. Here for the LP problem in the N-D space, the total number of intersection points formed by the $N+M$ hyper-planes is

$$C_{M+N}^N=C_{M+N}^M=\frac{(M+N)!}{N!\;M!}$$ (226)

The polytope enclosed by these $N+M$ hyper-planes is called the feasible region, in which the optimal solution must lie. The vertices of the polytopic feasible region are a subset of the $C_{M+N}^N$ intersections.

Fundamental theorem of linear programming

The optimal solution ${\bf x}^*$ of a linear programming problem formulated above is either a vertex of the polytopic feasible region $P$, or lies on a hyper-surface of the polytope, on which all points are optimal solutions.

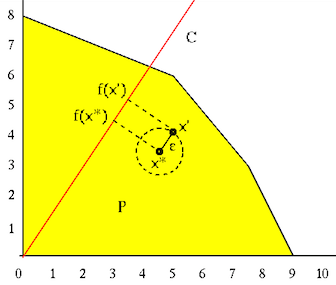
Proof:

Assume the optimal solution ${\bf x}^*\in P$ is interior to the polytopic feasible region $P$, then there must exist some $\epsilon>0$ such that the hyper-sphere of radius $\epsilon$ centered at ${\bf x}^*$ is inside $P$. Evaluate the objective function at a point on the hyper-sphere

$${\bf x}'={\bf x}^*+\epsilon\;{\bf c}/\vert\vert{\bf c}\vert\vert\in P$$ (227)

we get

$$f({\bf x}')={\bf c}^T{\bf x}' ={\bf c}^T({\bf x}^*+\epsilon\;{\bf... ...{\bf x}^*+\epsilon\;\vert\vert{\bf c}\vert\vert>{\bf c}^T{\bf x}^*=f({\bf x}^*)$$ (228)

i.e., ${\bf x}^*$ cannot be the optimal solution as assumed. This contradiction indicates that an optimal solution ${\bf x}^*$ must be on the surface of $P$, either at one of its vertices or on one of its surfaces. Q.E.D.

Based on this theorem, the optimization of a linear programming problem could be solved by exhaustively checking each of the $C_{N+M}^N$ intersections formed by $N$ of the $N+M$ hyper-planes to find (a) whether it is feasible (satisfying all $N+M$ constraints), and, if so, (b) whether the objective function $f({\bf x})$ is maximized at the point. Specifically, we choose $N$ of the $N+M$ equations for the the constraints and solve this N-equation and N-unknown linear system to get the intersection point of $N$ corresponding hyper-planes. This brute-force method is most straight forward, but the computational complexity is high when $N$ and $M$, and therefore $C_{N+M}^N$, become large.

Example:

$$\begin{tabular}{ll} max: & $f_p(x_1,x_2)=2x_1+3x_2$\ \\ s. t.: &... ...le 40 \\ x_1 \ge 0,\;\; x_2\ge 0 \end{array}\right.$ \end{tabular}\;\;\;\;\;\; \;\;\;\;\;\; \begin{tabular}{ll} max: & $f_p({\bf x})={\bf c}^T{\... ...{\bf x}-{\bf b}\le{\bf0}\\ {\bf x}\ge {\bf0} \end{array}\right.$ \end{tabular}$$

where

$${\bf x}=\left[\begin{array}{c}x_1\\ x_2\end{array}\right],\;\;\;\... ...ight],\;\;\;\; {\bf A}=\left[\begin{array}{cc}2&1\\ 6&5\\ 2&5\end{array}\right]$$

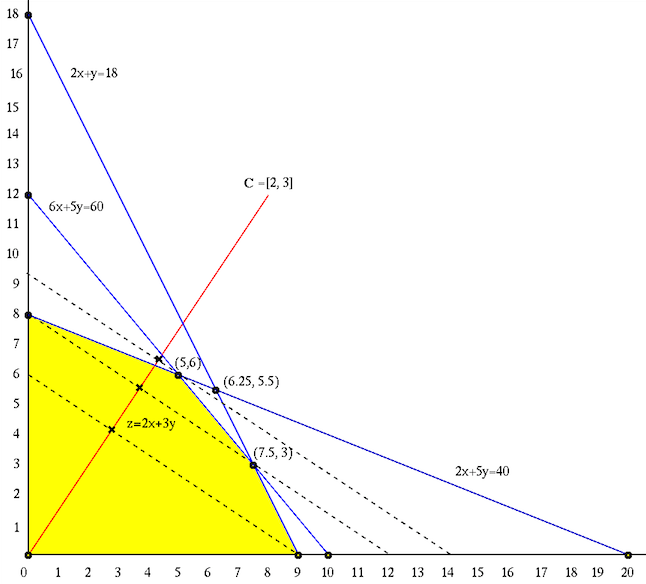
This problem has $N=2$ variables with the same number of non-negativity constraints and $M=3$ linear inequality constraints. The $n+m=5$ straight lines form $C_{N+M}^N=C_5^2=10$ intersections, out of which 5 are the vertices of the polygonal feasible region satisfying all constraints. The value of the objective function $f_p(x_1,x_2)={\bf c}^T{\bf x}=c_1x_1+c_2x_2$ is proportional to the projection of the 2-D variable vector ${\bf x}=[x_1,\;x_2]^T$ onto the coefficient vector ${\bf c}=[2,\;3]^T$. The goal of this linear programming problem is to find a point ${\bf x}$ inside the polygonal feasible region with maximum $f({\bf x})={\bf c}^T{\bf x}$ (the projection of ${\bf x}$ onto vector ${\bf c}$ if $\vert\vert{\bf c}\vert\vert=1$). Geometrically, this can be understood as to push the hyper-plane ${\bf c}^T{\bf x}=z$, here a line in 2-D space, its normal direction ${\bf c}$, away from the origin along to eventually arrive at the vertex of the polytopic feasible region farthest away from the origin.

This LP problem can be converted into the standard form:

$$\begin{tabular}{ll} max: & $f_p(x_1,x_2)=2x_1+3x_2$\ \\ s. t.: &... ...; x_2\ge 0,\; s_1\ge 0,\; s_2\ge 0,\; s_3\ge0 \end{array}\right.$ \end{tabular}$$

Listed in the table below are the $C_{M+N}^N=C_5^2=10$ intersections ${\bf x}$, called basic solutions, together with the corresponding slack variables $s_1,\,s_2,\,s_3$ and the objective function value $f({\bf x})$ (proportional to the projection of ${\bf x}$ onto ${\bf c}$). We see that out of the ten basic solutions, five are feasible (vertices of the polytopic feasible region) with all $M+N=5$ variables taking non-negative values, while the remaining five are not feasible, as some of the slack variables are negative, and thereby violating the constraints. Out of the five feasible solutions, the one at ${\bf x}^*=(5,\;6)$ is optimal with maximum objective function value $f_p(x_1,x_2)=2x_1+3x_2=2\times 5+3\times6=28$.

$$\begin{tabular}{c\vert\vert cc\vert ccc\vert\vert c\vert c}\hline... .../14.99 \\ 10& 0 & 0 & 18 & 60 & 40 & feasible & 0/0.00 \\ \hline \end{tabular}$$

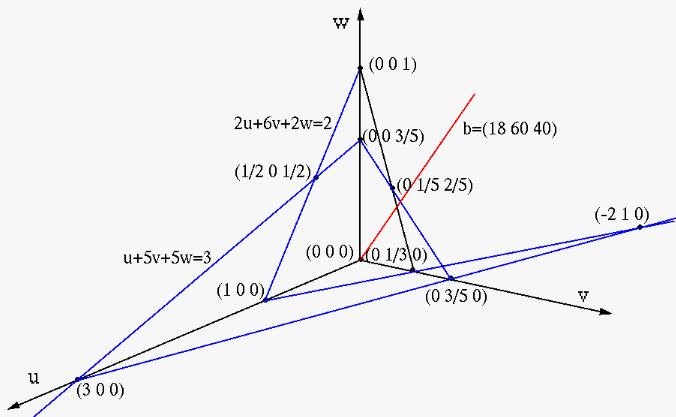
This primal maximization problem can be converted into the dual minimization problem:

$$\begin{tabular}{ll} min: & $f_d(y_1,y_2,y_3)=18y_1+60y_2+40y_3$\ ... ...y_1\ge 0,\;y_2\ge 0,\;y_3\ge 0\\ \end{array}\right.$ \end{tabular}\;\;\;\;\;\; \;\;\;\;\;\; \begin{tabular}{ll} min: & $f_d({\bf y})={\bf b}^T{\... ...{\bf y}-{\bf c}\ge{\bf0}\\ {\bf y}\ge {\bf0} \end{array}\right.$ \end{tabular}$$

The five planes, $m=2$ from the constraining inequalities, and $n=3$ for the non-negative constraints $y_1\le 0$, $y_2\le 0$, and $y_3\le 0$ for the three variables, form $10$ intersection points:

$$\begin{tabular}{c\vert c\vert c\vert c}\hline & $(y_1,\,y_2,\,y_3... ...,1,0) & infeasible & 24\\ 10 & (0,0,0) & infeasible & 0\\ \hline \end{tabular}$$

We see that at the feasible point $(0,1/5,2/5)$, the dual function $f_d(y_1,y_2,y_3)=18y_1+60y_2+40y_3$ is minimized to be $28$, the same as the maximum of the primal function $f_p(x_1,x_2)=2x_1+3x_2$ at $(5,6)$.

Homework:

Develop the code to find all $C_{N+M}^N$ intersections formed by $N+M$ given hyper-planes in an N-D space in terms of their equations ${\bf A}_{M\times N}{\bf x}_{N\times 1}\le{\bf b}_{M\times 1}$ and ${\bf x}\ge{\bf0}$, identify which of them are vertices of the polytope surrounded by these hype-planes, and find the vertex corresponding to the optimal solution that maximizes $f({\bf x})={\bf c}^T{\bf x}$ for a given ${\bf c}$.