Next: Duality and KKT Conditions Up: Constrained Optimization Previous: Optimization with Equality Constraints
The optimization problems subject to inequality constraints can be generally formulated as:
 |
(185) |
 and
and  , as shown in the figure below for the minimization
(left) and maximization (right) of
, as shown in the figure below for the minimization
(left) and maximization (right) of
 subject to
subject to
 . The constrained solution
. The constrained solution
![${\bf x}^*=[x^*_1,\,x^*_2]^T$](img691.svg) is on the boundary of the feasible region satisfying
is on the boundary of the feasible region satisfying
 ,
while the unconstrained extremum is outside the feasible region.
,
while the unconstrained extremum is outside the feasible region.
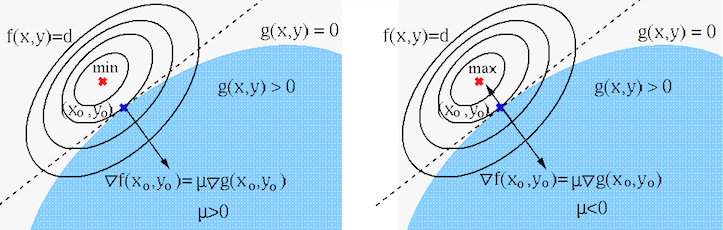
Consider the following two possible cases.
 is outside the feasible
region, i.e., the inequality constraint is active, then the
constrained solution
is outside the feasible
region, i.e., the inequality constraint is active, then the
constrained solution  must be
must be
 ,
,
 ;
;
 and the constraining function
and the constraining function
 to have the same tangent
at
to have the same tangent
at  , or parallel gradients:
, or parallel gradients:
 or or |
(186) |
 or
or  , respectively, as illustrated in the 1-D examples in
the figure below:
, respectively, as illustrated in the 1-D examples in
the figure below:
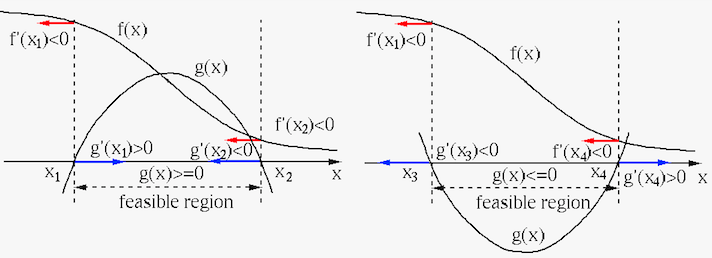
Depending on whether




 |
(187) |
 and
and
 for either maximization or minimization:
for either maximization or minimization:
 of this unconstrained
problem is
of this unconstrained
problem is
 ;
;
 ;
;
 and find the solution solving the
same equation
and find the solution solving the
same equation

Summarizing the two cases above, we see that




The discussion above can be generalized from 2-D to 




 |
(191) |
 indicated in Table 188
is negated.
indicated in Table 188
is negated.
We now set the gradient of the Lagrangian to zero:
![$\displaystyle \bigtriangledown_{{\bf x},{\bf\mu}} L({\bf x},{\bf\mu})
=\bigtria...
...bf x},{\bf\mu}}\left[f({\bf x})
-\sum_{i=1}^n\mu_i\,g_i({\bf x})\right]
={\bf0}$](img717.svg) |
(192) |
 and
and  equations,
respectively:
equations,
respectively:
 |
(193) |
 |
(194) |
The result above for the inequality constrained problems is the same
as that for the equality constrained problems considered before. However,
we note that there is an additional requirement regarding the sign of the
scaling coifficients. For an equality constrained problem, the direction
of the gradient



We now consider the general optimization of an N-D objective function

 |
(195) |
 equality and
inequality constraints in vector form as:
equality and
inequality constraints in vector form as:
 |
(196) |
![${\bf h}({\bf x})=[h_1({\bf x}),\cdots,h_m({\bf x})]^T$](img723.svg) and
and
![${\bf g}({\bf x})=[g_1({\bf x}),\cdots,g_n({\bf x})]^T$](img724.svg) .
.
To solve this optimization problem, we first construct the Lagrangian
 |
(197) |
![${\bf\lambda}=[\lambda_1,\cdots,\lambda_m]^T$](img677.svg) and
and
![${\bf\mu}=[\mu_1,\cdots,\mu_n]^T$](img726.svg) are for the
are for the  equality and
equality and  non-negative constraints, respectively, and then set its gradient with
respect to both
non-negative constraints, respectively, and then set its gradient with
respect to both
 and
and  as well as
as well as  to
zero. The solution
to
zero. The solution  can then be obtained by solving the
resulting equation system. While
can then be obtained by solving the
resulting equation system. While  can be either positive
or negative, with sign of
can be either positive
or negative, with sign of  needs to be consistent with those
specified in Table 188. Otherwise the inequality
constraints is inactive.
needs to be consistent with those
specified in Table 188. Otherwise the inequality
constraints is inactive.
Example:
Find the extremum of




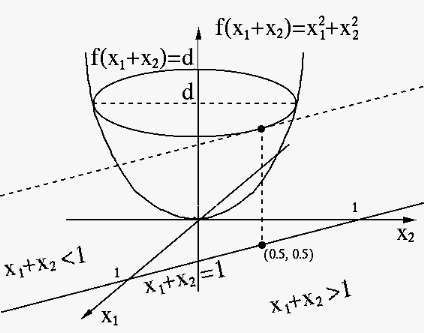
 |
 |
 |
 , i.e., the function
is minimized at
, i.e., the function
is minimized at
 . We note that
. We note that
 and
and
 have the same gradients:
have the same gradients:
![$\displaystyle \bigtriangledown f(0.5,0.5)=\bigtriangledown h(0.5,0.5)=[1,1]^T$](img742.svg) |
 |
 and
and  .
According to Table 188,
.
According to Table 188,  is
the solution for the minimization problem subject to
is
the solution for the minimization problem subject to
 (left), or the maximization problem
subject to
(left), or the maximization problem
subject to
 .
.
 |
 , and
, and  .
According to Table 188,
.
According to Table 188,  is
not the solution of either the maximization problem
subject to
is
not the solution of either the maximization problem
subject to
 (left), or the minimization
problem subject to
(left), or the minimization
problem subject to
 (right), i.e., the
constraint is inactive. We therefore need to assume
(right), i.e., the
constraint is inactive. We therefore need to assume  and solve the following equations for an unconstrained problem:
and solve the following equations for an unconstrained problem:
 |
 and
and
 , with
minimum
, with
minimum
 . This is the solution for the
minimization problem (right), at which
. This is the solution for the
minimization problem (right), at which
 ,
i.e., the constraint is inactive. However this is not
the solution for the maximization problem (left) as the
function is not bounded from above.
,
i.e., the constraint is inactive. However this is not
the solution for the maximization problem (left) as the
function is not bounded from above.