Reinforcement Learning

Reinforcement learning (RL) can be considered as one of the three basic machine learning paradigms, alongside supervised learning (e.g., regression and classification) and unsupervised learning (e.g., clustering) discussed previously. The goal of RL is for the algorithm, a software agent, to learn to make a sequence of decisions, called policy, for a specific task in a given environment, for the purpose of receiving the maximum rewards from the environment.

Different from supervised learning for either regression or classification based on a given training dataset composed of a set of i.i.d. sample points ${\bf x}_n$ labeled by $y_n,\; (n=1,\cdots,N)$, RL is a learning method without any examples of optimal behaviors. Instead, RL learns on its own without relying on any labeled training dataset explicitely informing the agent what the correct responses are while interacting with the environment. On the other hand, different from the unsupervised methods that learns passively from the given dataset, RL is a trial-and-error learning method, in which the agent actively interacts with and learns from the given environment.

Specifically, RL as a sequential method depends on the dynamics of the environment which is modeled by a Markov decision process (MDP), a stochatic system of multiple states with probabilistic state transitions and rewards. If the MDP model of the environment in terms of its the state transition and reward probabilities is known, the agaent only needs to find the optimal policy in terms of what action to take at each state of the MDP to achieve maximum accumulated rewards as the consequence of its actions. The task in this model-based case is called planning. On the other hand, if MDP of the environment is unknown, the agent needs to learn the environment by repeatedly running the dynamic process of the MDP based on some initial policy and gradually evaluate the received rewards and improve the policy to eventually reach optimality. The task in this model-free case is called control.

Depending on the action taken by the agent in the current state $s$, the system transits to the next state $s'$ following certain transition probability distribution. The RL is to choose the optial action in the current state, to maximize the long-term expected reward, as the feedback of the environment. This is typically carried out by dynamic programming (DP), a class of algorithms seeking to simplify a complex problem by breaking it up into a set of sub-problems which can be solved recursively.

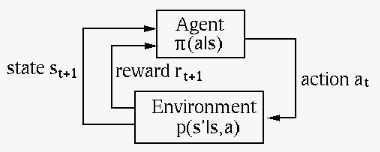
The figure below illustrates the basic concepts of RL, where the agent makes a decision in terms of the action $a_t$ to take in the current state $s_t$ by following some policy $\pi(a\vert s)$, while the environment makes a transition from the current state $s_t$ to the next state $s_{t+1}$ by following the transition probability, a conditional probability $p(s'\vert s, a)$ for the next state $s_{t+1}=s'$ given the curent state $s_t=s$ and the action $a_t$ taken by the agent, and provides a reward $r_{t+1}$.