


Next: About this document ...
Up: resize
Previous: Arbitrary resizing
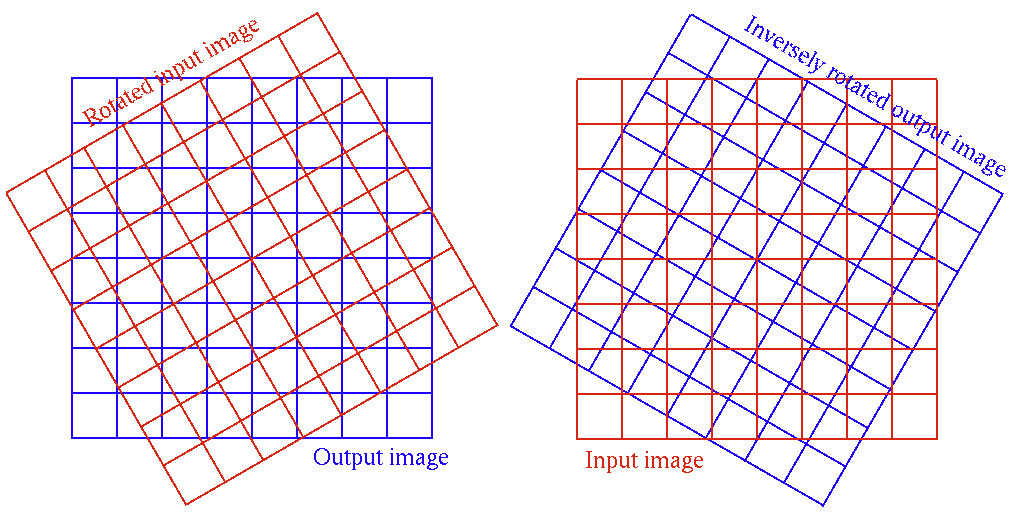
We first note that rotating the input image 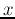 by an angle
by an angle 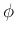 is equivalent
to rotating the output image
is equivalent
to rotating the output image 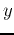 by an angle
by an angle 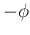 . For the indices
. For the indices 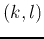 of
each pixel in the output
of
each pixel in the output 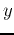 we find the corresponding position in the input
we find the corresponding position in the input 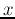 :
:
This rotation is about the origin of the image, the top left corner of the image.
If we want the rotation to be around the center
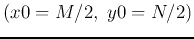 of an image
of size
of an image
of size 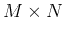 , then
, then
Next we find the interpolation value 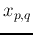 for each pixel
for each pixel 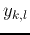 of the
output image using the same bilinear interpolation method as in the arbitrary
scaling discussed above. Note that some pixels in the image after the rotation
may be outside the original image before the rotation, they can be arbitrarily
assigned with any color, such as black.
of the
output image using the same bilinear interpolation method as in the arbitrary
scaling discussed above. Note that some pixels in the image after the rotation
may be outside the original image before the rotation, they can be arbitrarily
assigned with any color, such as black.

Ruye Wang
2014-09-12
![]() by an angle
by an angle ![]() is equivalent
to rotating the output image
is equivalent
to rotating the output image ![]() by an angle
by an angle ![]() . For the indices
. For the indices ![]() of
each pixel in the output
of
each pixel in the output ![]() we find the corresponding position in the input
we find the corresponding position in the input ![]() :
:
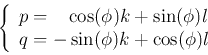
![\begin{displaymath}
\left\{ \begin{array}{l}
p=[\;\;\;\cos(\phi) (k-x0)+\sin(\p...
...-\sin(\phi) (k-x0)+\cos(\phi) (l-y0)]+y0
\end{array} \right.
\end{displaymath}](img58.png)

