Arbitrary resizing

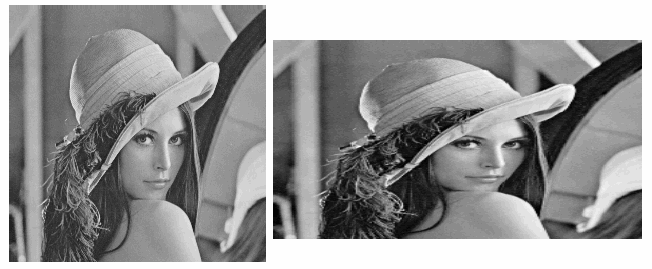
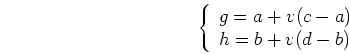It is obviously more desirable to arbitrarily resize a given image (enlarge or reduce the image proportionally or non-proportionally). We first consider converting a one-dimensional m-sample input $\{ x_i, (i=0, 1, \cdots, m-1) \}$ into an n-sample output $\{ y_j, (j=0, 1, \cdots, n-1) \}$, where $n$ is the desired size of the output, which may be either smaller or greater than $m$, i.e., the scaling factor $n/m$ can be either greater or smaller than 1 (for either enlargement or reduction). The method is essentially a two-step process of linear interpolation and re-sampling.

• Convert indices:

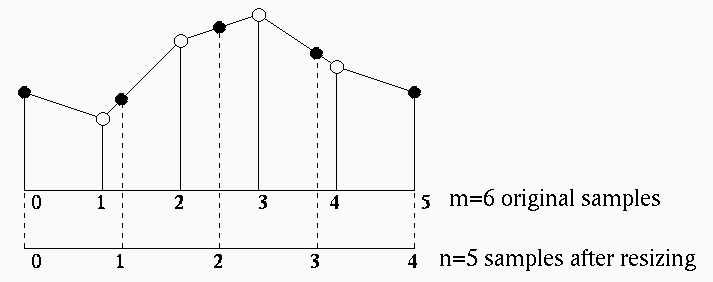
  Represent each index $0 \leq k \leq n-1$ of the output as a floating point number $p$ in the range of $0 \leq i \leq m-1$ of the input indices:
  

  $$\frac{p}{m-1}=\frac{k}{n-1},\;\;\;\;\;\mbox{i.e.}\;\;\;\; p=k\; \frac{m-1}{n-1}$$
  
  
  The indices of the two neighboring samples of $p$ can be found as
  
  $$i = \lfloor p \rfloor \;\;\leq\;\; p \;\;\leq \;\;\lceil p \rceil =i+1$$
  
  
  where $\lfloor p \rfloor$ and $\lceil p \rceil$ represent, respectively, the floor and the ceiling of $p$, i.e., the largest integer smaller than $p$ and the smallest integer larger than $p$.

• Re-sampling:

  Find the fraction $0 \leq (u=p-i) \leq 1$ and $d$ as shown in the figure:
  

  $$\frac{d}{u}=\frac{x_{i+1}-x_{i}}{(i+1)-i}=x_{i+1}-x_i,\;\;\;\;\mbox{i.e.,} \;\;\;\;\;\;d=u(x_{i+1}-x_i)$$
  
  
  Now the kth value $y_k$ of the output can be found as the interpolation between $x_i$ and $x_{i+1}$:
  
  $$y_k=x_{p}=x_i+d=x_i+u(x_{i+1}-x_i)$$
  
  

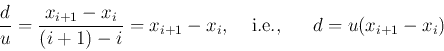
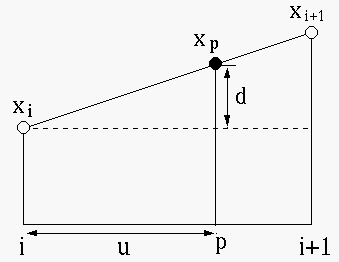
This method of linear interpolation can be generalized from 1-D to 2-D bilinear interpolation for image resizing.

• Convert indices:

  Similar to the 1D case, we first convert the integer indices $(k,l)$ of each pixel of the output image of the desired size into real coordinates $(p, q)$ in the range of the input image. Then the corresponding fractions $u$ and $v$ in both horizontal and vertical dimensions can be found:
  

  $$i = \lfloor p \rfloor, \;\;\;\;\; i+1=\lceil p \rceil, \;\;\;\;\; u=p-i$$
  
  
  
  
  $$j = \lfloor q \rfloor, \;\;\;\;\; j+1=\lceil q \rceil, \;\;\;\;\; v=q-j$$
  
  

• Re-sampling:

  Find value $x_{p,q}$ as the bilinear interpolation of its four immediate neighbors in the input image, represented by
  

  $$a=x_{i,j},\;\;\;\;\;\; b=x_{i+1,j},\;\;\;\;\;\; c=x_{i,j+1},\;\;\;\;\;\; d=x_{i+1,j+1}$$
  
  

  

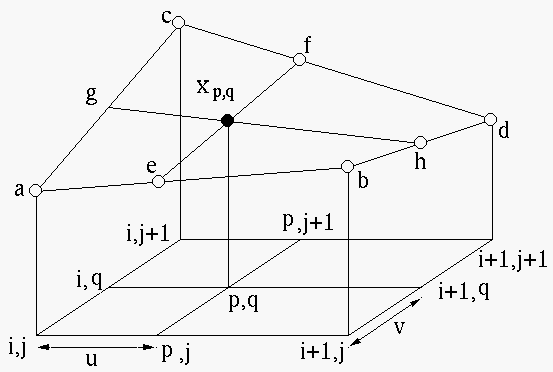
  The bilinear interpolation is carried out in two levels of linear interpolations. We first find the two interpolations of $a$, $b$ and $c$, $d$ along the dimension with index $i$:
  

  $$\left\{ \begin{array}{ll} e=a+u(b-a) f=c+u(d-c) \end{array} \right.$$
  
  
  and then find $y_{k,l}=x_{p,q}$ as the linear interpolation of e and f along the dimension with index $j$:
  
  $$y_{k,l}=x_{p,q}=e+v(f-e)=(1-u-v+uv)a+u(1-v)b+v(1-u)c+uvd$$
  
  
  Alternatively and equivalently, we could first find the interpolations along the dimension in $j$:
  
  $$\left\{ \begin{array}{ll} g=a+v(c-a) h=b+v(d-b) \end{array} \right.$$
  
  
  and then find the pixel value of the output as the interpolation along the dimension in $i$: The result is exactly the same as before.