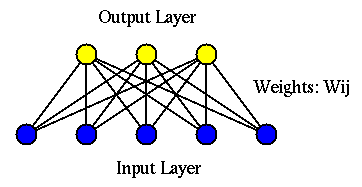
A perceptron network (F. Rosenblatt, 1957) also has 2 layers as in the previous Hebb's network, except the learning law is different. This is a supervised learning algorithm based on some prior knowledge.

We first consider the case in which there is only ![]() output node in the
network. Presented with a pattern vector
output node in the
network. Presented with a pattern vector
![]() , the
output is computed to be
, the
output is computed to be
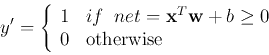
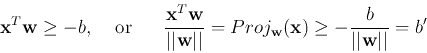
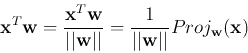
The binary output ![]() is either
is either ![]() indicating
indicating ![]() belongs to class 1
(
belongs to class 1
(
![]() ) or
) or ![]() indicating
indicating ![]() belongs to class 2
(
belongs to class 2
(
![]() ), i.e.,
), i.e.,
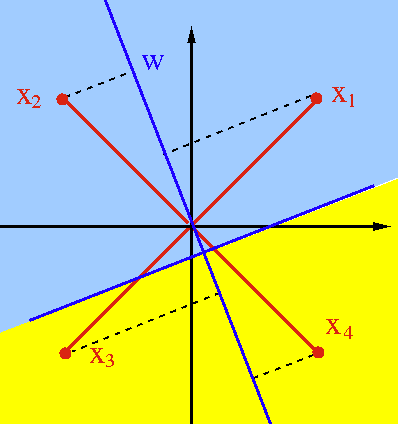
The weight vector ![]() is obtained in the training process based on a set
of
is obtained in the training process based on a set
of ![]() training samples with known classes (labeled):
training samples with known classes (labeled):
![]() , where
, where ![]() is an n-D vector representing a pattern and
the binary label
is an n-D vector representing a pattern and
the binary label ![]() indicates to which one of the two classes
indicates to which one of the two classes ![]() or
or
![]() the input
the input ![]() belongs.
belongs.
Specifically, in each step of the training process, one of the ![]() patterns
patterns
![]() randomly chosen is presented to the
randomly chosen is presented to the ![]() input nodes for the network
to generate an output
input nodes for the network
to generate an output ![]() . This output is then compared with the the desired
output
. This output is then compared with the the desired
output ![]() corresponding to this input to obtain their difference
corresponding to this input to obtain their difference ![]() ,
based on which the weight vector
,
based on which the weight vector ![]() is then updated by the following
learning law:
is then updated by the following
learning law:
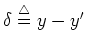 represents the error, the difference
between the actual output and the desired output, and the learning law is called
the
represents the error, the difference
between the actual output and the desired output, and the learning law is called
the
Perceptron convergence theorem:
Ifand
are two linearly separable clusters of patterns, then a perceptron will develop a
in finite number of training trials to classify them.
As the perceptron network is only capable of linear operations, the
corresponding classification is limited to classes that are linearly
separable by a hyperplane in the n-D space. A typical example of two
classes not linearly separable is the XOR problem, where the 2-D space
is divided into four regions for two classes 0 and 1, just like the
Karnaugh map for the exclusive-OR of two logical variables ![]() .
.
When there are ![]() output nodes in the network, the network becomes a
multiple-class classifier. The weight vectors
output nodes in the network, the network becomes a
multiple-class classifier. The weight vectors ![]() (
(![]() )
for these
)
for these ![]() output nodes define
output nodes define ![]() hyperplanes that partition the n-D
space into multiple regions each corresponding to one of the classes.
Specifically, if
hyperplanes that partition the n-D
space into multiple regions each corresponding to one of the classes.
Specifically, if ![]() , then the n-D space can be partitioned into as
many as
, then the n-D space can be partitioned into as
many as ![]() regions.
regions.
The limitation of linear separation could be overcome by having more than one learning layer in the network. However, the learning law for the single-layer perceptron network no longer applies. New training method is needed.