Donald Hebb (Canadian Psychologist) speculated in 1949 that
``When neuron A repeatedly and persistently takes part in exciting neuron B, the synaptic connection from A to B will be strengthened.''Simultaneous activation of neurons leads to pronounced increases in synaptic strength between them. In other words, "Neurons that fire together, wire together. Neurons that fire out of sync, fail to link". So a Hebbian network can be used as an associator which will establish the association between two sets of patterns
The classical conditioning (Pavlov, 1927) could be explained by Hebbian learning:
The structure
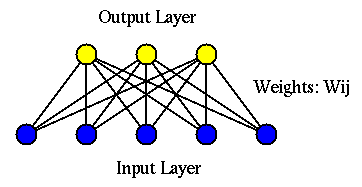
The Hebbian network model has an n-node input layer
![]() and an m-node output layer
and an m-node output layer
![]() . Each output node is
connected to all input nodes:
. Each output node is
connected to all input nodes:
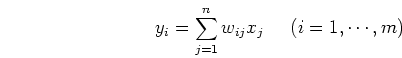
The learning law
Training
If we assume ![]() initially,
initially, ![]() and a set of
and a set of ![]() pairs of patterns
pairs of patterns
![]() are presented repeatedly during
training, we have
are presented repeatedly during
training, we have
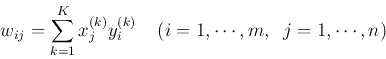
![\begin{displaymath}
{\bf W}_{m\timex n}=\sum_{k=1}^K {\bf y}_k {\bf x}_k^T = \s...
...m^{(k)} \end{array} \right]
[ x_1^{(k)}, \cdots, x_n^{(k)} ]
\end{displaymath}](img56.png)
Classification
When presented with one of the patterns ![]() , the network will produce
the output:
, the network will produce
the output:
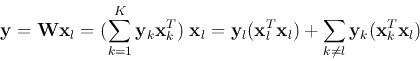
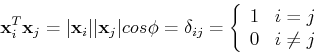
This condition implies that the ![]() input patterns are totally unrelated
to each other. Intuitively, how much two vectors are related to each other
can be measured by the angle
input patterns are totally unrelated
to each other. Intuitively, how much two vectors are related to each other
can be measured by the angle ![]() between them. If
between them. If ![]() is close to 0
the two vectors are closely related, because their elements are very similar
to each other so that they almost coincide. When negative values are allowed
for the elements and
is close to 0
the two vectors are closely related, because their elements are very similar
to each other so that they almost coincide. When negative values are allowed
for the elements and ![]() is close to 180 degrees, the vectors are also
highly related because their elements are the opposite of each other. In
either case, the
is close to 180 degrees, the vectors are also
highly related because their elements are the opposite of each other. In
either case, the ![]() is close to 1 and the inner product is maximized
indicating that the two vectors are either positively or negatively related
to each other. On the other hand, if the two vectors are perpendicular to each
other (
is close to 1 and the inner product is maximized
indicating that the two vectors are either positively or negatively related
to each other. On the other hand, if the two vectors are perpendicular to each
other (![]() ,
, ![]() ), the inner product of the two vectors is
very small or even zero indicating the elements of the a vector are irrelevant
to those of the other vector.
), the inner product of the two vectors is
very small or even zero indicating the elements of the a vector are irrelevant
to those of the other vector.
How much two patterns ![]() and
and ![]() are related to each other can
also be measured quantitatively, we define correlation coefficient as:
are related to each other can
also be measured quantitatively, we define correlation coefficient as:
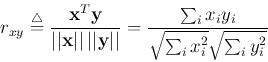
|
|
if |
| if |
|
|
|
if |
This condition implies that the capacity of the network (![]() input nodes)
is large enough for representing
input nodes)
is large enough for representing ![]() different patterns. This can be
translated into mathematical language that there can be no more than
different patterns. This can be
translated into mathematical language that there can be no more than ![]() orthogonal vectors in an n-D space.
orthogonal vectors in an n-D space.
If these conditions are true, then the response of the network to ![]() will be
will be
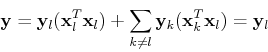
Although two patterns ![]() and
and ![]() don't have causal relationship
(as
don't have causal relationship
(as ![]() is caused by another pattern
is caused by another pattern ![]() ), but if they always appear
simultaneously, an association relationship can be established in the Hebbian
network.
), but if they always appear
simultaneously, an association relationship can be established in the Hebbian
network.