


Next: Competitive Learning Networks
Up: Introduction to Neural Networks
Previous: Summary of BP training
The radial basis function (RBF) networks are inspired by biological neural
systems, in which neurons are organized hierarchically in various pathways
for signal processing, and they tuned to respond selectively to different
features/characteristics of the stimuli within their respective fields.
In general, neurons in higher layers have larger receptive fields and they
selectively respond to more global and complex patterns.
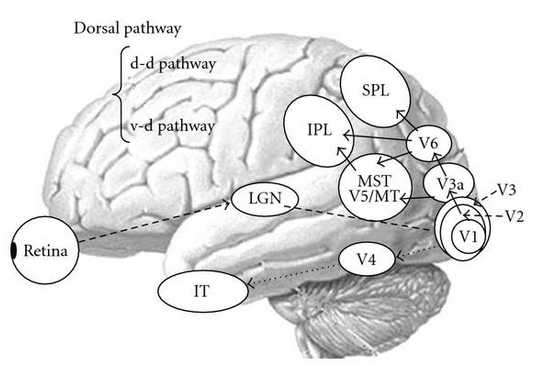
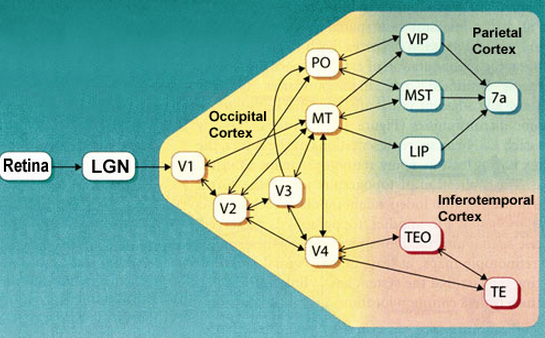
For example, neurons at different levels along the visual pathway respond
selectively to different types of visual stimuli:
- Neurons in the primary visual cortex (V1) receive visual input from
the retina and selectively respond to different
orientations
of linear features;
- Neurons in the middle temporal (MT) area receive visual input from
the V1 area and selectively respond to different
motion directions;
- Neurons in the medial superior temporal area (MST) receive visual input
from the MT area and selectively respond to different
motion patterns (optic flow)
such as rotation, expansion, contraction, and spiral motions.
Moreover, neurons in the auditory cortex respond selectively to different
frequencies.
The tuning curves,
the local response functions, of these neurons are typically Gaussian, i.e.,
the level of response is reduced when the stimulus becomes less similar to
what the cell most is most sensitive and responsive to (the most preferred).
These Gaussian-like functions can also be treated as a set of basis functions
(not necessarily orthogonal and over-complete) that span the space of all input
patters. Based on such local features represented by the nodes, a node in a
higher layer can be trained to selectively respond to some patterns/objects
(e.g., ``grandmother cell''),
based on the outputs of the nodes in the lower layer.
Applications:
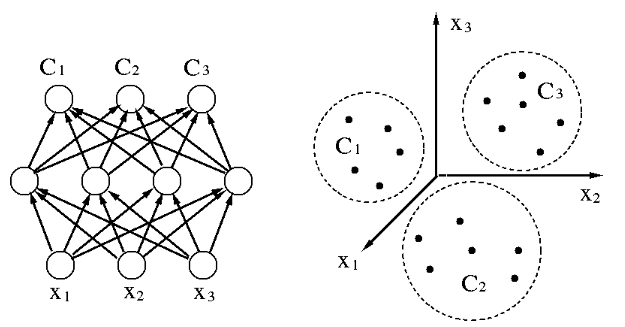
- The RBF network can be used in pattern classification, by which a given
pattern vector
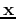 is classified into one of classes. The classification
is typically supervised, i.e., the network is trained based on a set of
is classified into one of classes. The classification
is typically supervised, i.e., the network is trained based on a set of 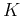 training patterns
training patterns
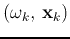 (
(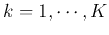 ), where
), where 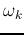 indicates the class the kth pattern
indicates the class the kth pattern 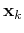 belongs, i.e.,
belongs, i.e.,
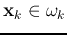 .
.
- RBF networks can also be used for non-parametric regression.
In parametric regression, the form of the function of interest is known,
such as linear regression,
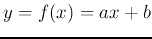 . All we need to do is to find a set
of parameters, e.g.,
. All we need to do is to find a set
of parameters, e.g., 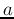 and
and 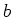 , based on the observed data
, based on the observed data 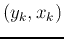 (
(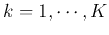 ). However, in non-parametric regression, little knowledge
is available regarding the type and form of the function
). However, in non-parametric regression, little knowledge
is available regarding the type and form of the function 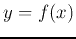 . For example,
in time-series predicting, the value
. For example,
in time-series predicting, the value 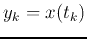 of a time series can be
estimated/predicted from the
of a time series can be
estimated/predicted from the 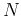 previous values
previous values
![${\bf x}_k=[x(t_{k-1}),\;x(t_{k-2}),\cdots,x(t_{k-N})]^T$](img263.png) based on
based on 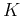 observations
observations
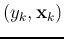 (
(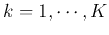 ).
This problem can also be viewed as fitting a hyper-surface
).
This problem can also be viewed as fitting a hyper-surface
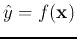 in an N-dimensional space to a set of
in an N-dimensional space to a set of 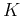 data
points
data
points
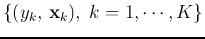 .
.
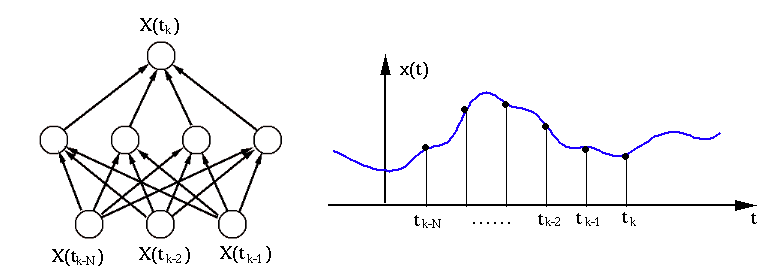
As seen in the examples above, an RBF network is typically composed of three
layers, the input layer composed of 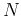 nodes that receive the input signal
nodes that receive the input signal
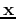 , the hidden layer composed of
, the hidden layer composed of 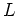 nodes that simulate the neurons
with selective tuning to different features in the input, and the output
layer composed of
nodes that simulate the neurons
with selective tuning to different features in the input, and the output
layer composed of 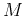 nodes simulating the neurons at some higher level that
respond to features at a more global level, based on the output from the
hidden layer representing different features at a local level. (This could
be considered as a model for the visual signal processing in the pathway
nodes simulating the neurons at some higher level that
respond to features at a more global level, based on the output from the
hidden layer representing different features at a local level. (This could
be considered as a model for the visual signal processing in the pathway
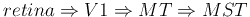 .)
.)
Upon receiving an input pattern vector 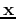 , the jth hidden node reaches
the activation level:
, the jth hidden node reaches
the activation level:
where 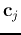 and
and 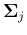 are respectively the mean vector and
covariance matrix associated with the jth hidden node. In particular, the covariance
matrix is a special diagonal matrix
are respectively the mean vector and
covariance matrix associated with the jth hidden node. In particular, the covariance
matrix is a special diagonal matrix
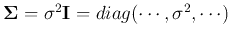 , then the Gaussian function becomes isotropic and we have
, then the Gaussian function becomes isotropic and we have
We see that 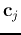 represents the preferred feature (orientation,
motion direction, frequency, etc.) of the jth neuron. When
represents the preferred feature (orientation,
motion direction, frequency, etc.) of the jth neuron. When
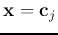 ,
the response of the neuron is maximized due to the selectivity of the neuron.
,
the response of the neuron is maximized due to the selectivity of the neuron.
In the output layer, each node receives the outputs of all nodes in the hidden
layer, and the output of the ith output node is the linear combination of the
net activation:
Note that the computation at the hidden layer is non-linear but that at the
output layer is linear, i.e., this is a hybrid training scheme.
Learning Rules
Through the training stage, various system parameters of an RBF network will
be obtained, including the 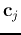 and
and 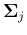 (
(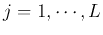 )
of the
)
of the 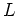 nodes of the hidden layer, as well as the weights
nodes of the hidden layer, as well as the weights 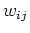 (
(
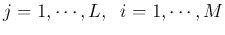 ) for the
) for the 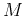 nodes of the output layer, each
fully connected to all
nodes of the output layer, each
fully connected to all 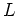 hidden nodes.
hidden nodes.
- Training of the hidden layer
The centers 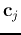 (
(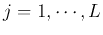 ) of the
) of the 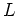 nodes of the hidden
layer can be obtained in different ways, so long as the entire data space
can be well represented.
nodes of the hidden
layer can be obtained in different ways, so long as the entire data space
can be well represented.
- They can be chosen randomly from the input data set
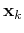 (
(
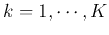 ).
).
- The centers can be obtained by unsupervised learning (SOM, k-means
clustering) based on the training data.
- The covariance matrix
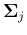 as well as the center
as well as the center 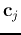 can also be obtained by supervised learning.
can also be obtained by supervised learning.
- Training of the output layer
Once the parameters 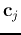 and
and 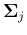 are available, we
can concentrate on finding the weights
are available, we
can concentrate on finding the weights 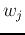 of the output layer, based on
the given training data containing
of the output layer, based on
the given training data containing 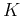 data points
data points
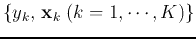 , i.e., we need to solve the equation system for the
, i.e., we need to solve the equation system for the 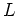 weights
weights 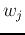 (
(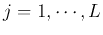 ):
):
This equation system can also be expressed in matrix form:
where
![${\bf y}=[y_1,\cdots,y_K]^T$](img281.png) ,
,
![${\bf w}=[w_1,\cdots w_L]^T$](img282.png) , and
, and  is an
is an 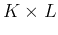 matrix function of the
matrix function of the 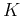 input vectors
input vectors 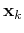 :
:
As the number of training data pairs 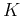 is typically much greater than
the number of hidden nodes
is typically much greater than
the number of hidden nodes 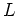 , the equation system above contains more
equations than unknowns, and has no solution. However, we can still try
to find an optimal solution so that the actual output
, the equation system above contains more
equations than unknowns, and has no solution. However, we can still try
to find an optimal solution so that the actual output
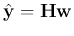 approximates
approximates 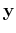 with a minimal mean squared
error (MSE):
with a minimal mean squared
error (MSE):
To find the weights as the parameters of the model, the
general linear least squares
can be used, based on the pseudo inverse of the non-square matrix:
In some cases (e.g., for the model of 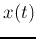 to be smooth), it is
desirable for the weights to be small. To achieve this goal, a cost
function can be constructed with an additional term added to the MSE:
to be smooth), it is
desirable for the weights to be small. To achieve this goal, a cost
function can be constructed with an additional term added to the MSE:
As shown in Appendix B, the
optimal solution of this system is



Next: Competitive Learning Networks
Up: Introduction to Neural Networks
Previous: Summary of BP training
Ruye Wang
2015-08-13






![]() nodes that receive the input signal
nodes that receive the input signal
![]() , the hidden layer composed of
, the hidden layer composed of ![]() nodes that simulate the neurons
with selective tuning to different features in the input, and the output
layer composed of
nodes that simulate the neurons
with selective tuning to different features in the input, and the output
layer composed of ![]() nodes simulating the neurons at some higher level that
respond to features at a more global level, based on the output from the
hidden layer representing different features at a local level. (This could
be considered as a model for the visual signal processing in the pathway
nodes simulating the neurons at some higher level that
respond to features at a more global level, based on the output from the
hidden layer representing different features at a local level. (This could
be considered as a model for the visual signal processing in the pathway
![]() .)
.)
![]() , the jth hidden node reaches
the activation level:
, the jth hidden node reaches
the activation level:
![\begin{displaymath}
f_i({\bf x})=\sum_{j=1}^L w_{ij} h_j({\bf x})
=\sum_{j=1}^L ...
...-({\bf x}-{\bf c}_j)^T {\bf\Sigma}_j^{-1}({\bf x}-{\bf c}_j)]
\end{displaymath}](img274.png)
![]() and
and ![]() (
(![]() )
of the
)
of the ![]() nodes of the hidden layer, as well as the weights
nodes of the hidden layer, as well as the weights ![]() (
(
![]() ) for the
) for the ![]() nodes of the output layer, each
fully connected to all
nodes of the output layer, each
fully connected to all ![]() hidden nodes.
hidden nodes.
![]() (
(![]() ) of the
) of the ![]() nodes of the hidden
layer can be obtained in different ways, so long as the entire data space
can be well represented.
nodes of the hidden
layer can be obtained in different ways, so long as the entire data space
can be well represented.
![]() and
and ![]() are available, we
can concentrate on finding the weights
are available, we
can concentrate on finding the weights ![]() of the output layer, based on
the given training data containing
of the output layer, based on
the given training data containing ![]() data points
data points
![]() , i.e., we need to solve the equation system for the
, i.e., we need to solve the equation system for the ![]() weights
weights ![]() (
(![]() ):
):
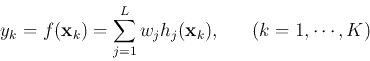
![\begin{displaymath}
{\bf H}=\left[\begin{array}{ccc}h_1({\bf x}_1)&\cdots&h_1({...
...bf x}_1)&\cdots&h_L({\bf x}_K) \end{array}\right]_{L\times K}
\end{displaymath}](img285.png)
![\begin{displaymath}
MSE=\vert\vert{\bf y}-\hat{\bf y}\vert\vert^2=\vert\vert{\b...
...m_{k=1}^K \left[y_k-\sum_{j=1}^L w_j h_j({\bf x}_k)\right]^2
\end{displaymath}](img287.png)
![]() to be smooth), it is
desirable for the weights to be small. To achieve this goal, a cost
function can be constructed with an additional term added to the MSE:
to be smooth), it is
desirable for the weights to be small. To achieve this goal, a cost
function can be constructed with an additional term added to the MSE: