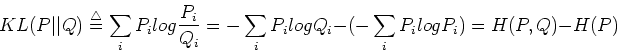Next: Appendix B: Matrix Operations
Up: MCMC and EM Algorithms
Previous: EM Method for Parameter
The KL-divergence between two distributions 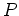 and
and 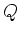 is defined as
is defined as
where 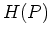 is the entropy of distribution
is the entropy of distribution 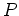 ,
, 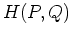 is the cross-entropy
of distributions
is the cross-entropy
of distributions 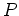 and
and 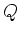 , and their difference, also called relative
entropy, represents the divergence or difference between the two distributions.
According Gibbs' inequality,
, and their difference, also called relative
entropy, represents the divergence or difference between the two distributions.
According Gibbs' inequality,
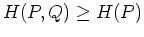 , with the equality holds
, with the equality holds
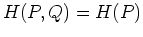 if and only if
if and only if 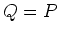 . Therefore
. Therefore
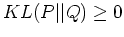 .
.
Ruye Wang
2006-10-11
![]() and
and ![]() is defined as
is defined as